Contents
Problem
Sometimes, a problem has sequential dependencies that cannot be broken. However, it is possible that many of the dependencies do not manifest themselves for most inputs and can be fixed up later even if ignored. How can concurrency be exploited in such problems efficiently?
Context
Consider the case where a problem contains a potentially large number of tasks that can usually run concurrently; however, for a subset of the tasks unpredictable dependencies emerge and these make it impossible to safely let the full set of tasks run concurrently. An effective solution may be to just run the tasks independently, that is speculate that concurrent execution will be committed, and then clean up after the fact any cases where concurrent execution was incorrect.
In many problems, there are long chains of sequential dependencies. This makes it especially hard to implement these problems on parallel hardware. One way to help parallelize such problems would be to break the dependency chain somehow. Breaking the chain through the use of speculation is one possible way to achieve parallel implementation.
The main insight to parallelize these problems is to observe that such dependencies are not essential most of the time. Depending on the input data, it might so happen that the dependent chains are not really dependent – they can be broken down into smaller independent tasks. After this decomposition, the problem can run efficiently on parallel processors. But, once in a while, an input data pattern might push the execution into a state where the dependency becomes crucial. In such cases, we might not be much better off than a serial algorithm, but on average we will be able to take advantage of the available hardware parallelism.
Speculation is usually a good source of macro level parallelism i.e. upto 10’s of macro level tasks. In order to scale to 100’s or 1000’s of processors, it is usually necessary to parallelize the tasks themselves.
Speculation can be used with the event based implicit invocation structural pattern. Computational patterns like Finite State Machines (FSM) and Backtrack Branch and Bound are good sources of problems on which speculation can be applied as a parallel algorithmic strategy.
Forces
Universal Forces
- Size of chunks vs. concurrency – Breaking the dependency chain into large number of independent tasks increases parallelism, but only when the decomposition is valid. In the worst case, this leads to a large amount of unnecessary work and can be very inefficient
- Cost of wrong speculation vs. exploitable concurrency – Depending on what the cost of speculating wrongly is, one has to tradeoff exploitable concurrency in the problem. Exposing too much concurrency can lead to a lot of wasted work, fixing up for specific inputs. Too much serialization results if not much of the concurrency is exploited
Implementation Forces
- Polling vs. interrupts for termination – Threads, which are speculatively executed, need to check if they are valid before committing their results. This checking can be done through polling or through interrupts, depending on the problem specifics.
Solution
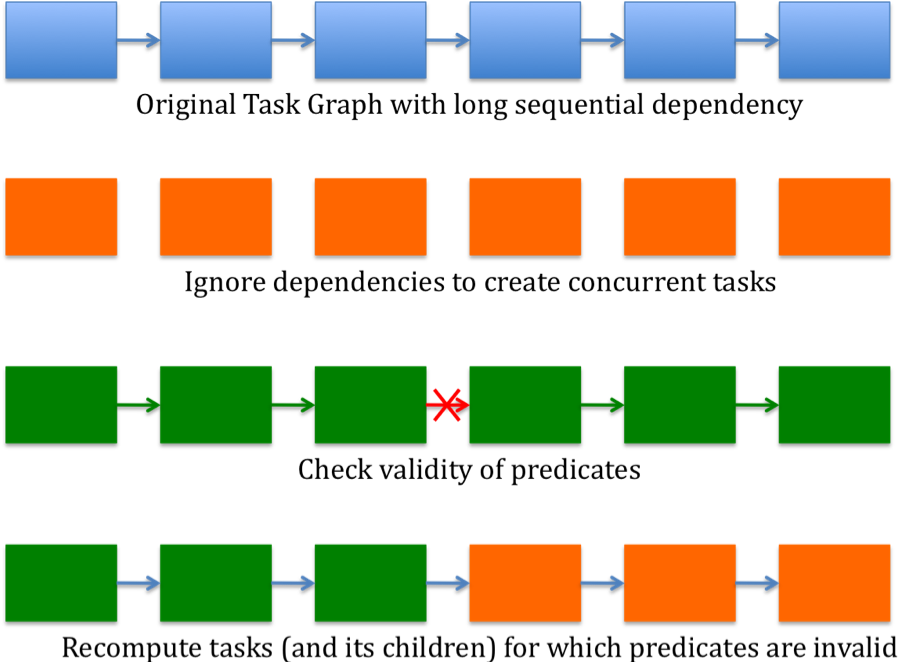
A solution to speculatively executing an algorithm involves the following steps:
- Task creation and predicate generation (break the dependency chain by ignoring dependencies)
- Mechanisms to check if the predicate is true/false
- Have a commit/recovery mechanism depending on whether the predicate was true/false respectively.
- Perform further optimizations (optional)
A discussion of each of the components in detail follows:
- Task creation and predicate generation
The main assumption in the speculation algorithmic strategy pattern is that we can break long dependency chains by ignoring them. Creating independent tasks is then a speculative action as ignoring these dependencies may not always hold good for all inputs. In order to detect such cases, we have to keep track of what needs to be true for the decomposition to hold. We call these conditions predicates.
Predicates may be generated statically or dynamically.
- In static generation, the thread that decides to start a speculative computation knows what the predicates are before the speculative thread starts execution. This is easy to manage as the creator thread performs all thread management. When it receives information about validity/invalidity of the predicates, it can accept the results of the speculated thread or terminate it.
- In dynamic generation, the thread that starts a speculative computation does not know what the predicates would be. They become known as the computation proceeds and are generated dynamically. Thread management is harder in these cases as there is not one thread that can keep track of the predicates.
An important decision to be made at this stage is that of task granularity. Smaller tasks usually lead to better dynamic load balancing and better utilization of parallel hardware resources. However, in our case, it can also lead to more wasted work and energy inefficiency. If some decisions are more important than others, then it might be better not to ignore those dependencies and not to split the tasks. This is a problem specific decision that depends on the nature of the algorithm being implemented.
For example, in parallelizing hard combinatorial problems like Boolean Satisfiability (SAT), it is common to parallelize the problem by executing the same problem with different heuristics and killing the other speculative threads when one of them finishes execution. This is done because it is hard to decide which of the heuristics would work best for a given problem and parallelizing each instance of the problem has proved to be difficult. Speculation is effective because picking the right heuristic can be orders of magnitude better than other heuristics. The predicate here is simple – the task that finishes first has a valid predicate and other tasks have their predicates invalidated.
2. Checking predicate validity
After tasks are created speculatively, it is necessary to check the validity of the tasks by checking the validity of their predicates. This is the crux of this algorithmic pattern, as it is in essence a non-work efficient pattern i.e it might do more work than is absolutely needed to solve a problem. Those threads whose predicates turn out to be false do the unnecessary work. A quick way of checking the predicate validity is therefore essential.
Predicate validity check is a very important aspect of this pattern. We can assume that the information for validating the predicates is not available when the speculative tasks are created (If such information exists, it makes no sense to speculate). Hence, that information is obtained only after the speculative tasks start execution.
Depending on the static/dynamic creation of predicates, the software architecture for performing this stage varies a lot. In the dynamic case where the predicates themselves are generated during the computations, an event-based implicit invocation like software architecture or an agent-and-repository like software architecture works best. With an event-based implicit invocation structure, the speculative tasks can “register” their predicates as events and can be notified when other threads update such information. With an agent-and-repository structure, the speculative threads can be thought of as agents querying the repository for the information they need to validate their predicates. This shows the two different styles for waiting on information in general – interrupt versus polling based approaches. Interrupt based approaches work best with an event-based implicit invocation-like software architecture while polling approaches can use an agent-and-repository like software architecture with a generic shared data implementation
3. Commit/recovery mechanism
Once we have validated the predicates, we need mechanisms to recover if the predicates are invalid. If the predicates turn out to be true, one usually also checks to make sure that its parental task(s) has committed before committing itself. When the predicate is invalid, there are two approaches:
- The computation done is wrong and should not be committed
- The computation done is redundant/unnecessary and need not be committed (committing is wasteful, but does not produce any wrong results)
Case 2 is simple, as we can just let the thread run to completion. With case 1, however, we need to make sure that the speculative thread has not modified any shared state before destroying it. If it has modified the shared state, we have to restore it back to a “correct” state. If the shared state modifications done at small scales (i.e at word level), hardware mechanisms like transactional memory might help (as long as all the shared state modifications are in a critical section). Some speculation can be automatically done by hardware – e.g. branch prediction in CPU.
Recovery mechanism involves recomputing all the tasks and their children whose predicates are known to be invalid. Thus, the worst-case complexity of speculation as a parallel algorithm strategy is not better than the sequential case. If there are inputs that will trigger all the dependencies, then we cannot do better than the serial version using naïve speculation. However, it might still be possible to do better by using intelligent recovery mechanisms.
If the dependencies are localized i.e. the validity of each task depends only on the validity of the previous few tasks and not on the tasks further up the dependency chain, we could attain better performance. In such cases, an invalid predicate would only invalidate that particular task and a few tasks downstream, but not all the other children. This is possible if we can make claims about the validity of each task as a function of the validity of its parent (and possibly a few more ancestor) tasks.
We can use the task queue pattern to get an implementation of the speculation pattern in source code. If we use the task queue implementation pattern, information needs to be given to the task queue, so that locality is exploited. Executing tasks that are localized in the dependency graph leads to less wasted work and better efficiency. Executing tasks that are close in the dependency graph provides the benefits of early validity detection, thereby saving work if the predicates turn out to be invalid. Usually, task queue systems do not support task termination other than the normal exit at the end of execution. To obtain the benefits of speculation, it is necessary for the task queue system to support polling/interrupt-based task termination.
4. Optimization
Optimization can be done using general task parallelism optimization techniques (load balancing, communication avoidance etc.) This mostly reduces to making sure that the speculative tasks are of almost the same size, avoiding breaking dependencies that might be too expensive to patch up later and coming up with efficient ways to validate predicates and recover if invalid.
Figure 1. Speculation
Speculation is also a concurrent execution pattern. Such low level speculation is usually handled by the hardware and can be efficient in some cases. The simplest example of hardware speculation is branch predication, which is present in almost all major desktop CPUs. With branch predication, for each branch instruction, one path is speculatively chosen based on the past behavior of the program. This can be extended to speculatively execute both branches and terminate one of them when the result of the branch predicate is available. However, this is at a much finer granularity (only a few instructions). Speculation as a parallel algorithmic strategy is usually at a much higher granularity and managed by the software developers.
Invariant
- The invariant structure should be able to confirm that the dependency break is valid if the predicates are valid. If this is not true, it can be verified by writing test cases where the dependencies have to be met and seeing if the predicates capture all this information.
- If the particular problem instance exploits the property that not all descendents of a task have to be invalidated if it gets invalidated, assertions/test cases should verify this.
Examples
Parallelizing a HTML Lexical Analyzer
Lexical analysis is the process of converting a sequence of characters into a sequence of tokens. Programs performing lexical analysis are called lexical analyzers or lexers. Consider we are lexing HTML documents. We need to identify each token (lexeme) from inputstring in the documents based on the HTML tag specifications. Suppose the specifications are given as:
Content ::= one or more characters that are not ‘<’
EndTag ::= ‘<’ , ‘/’ followed by zero or more characters that are not ‘>’ and ending with ‘>’
StartTag ::= ‘<’ followed by zero or more characters that are not ‘>’ and ending with ‘>’
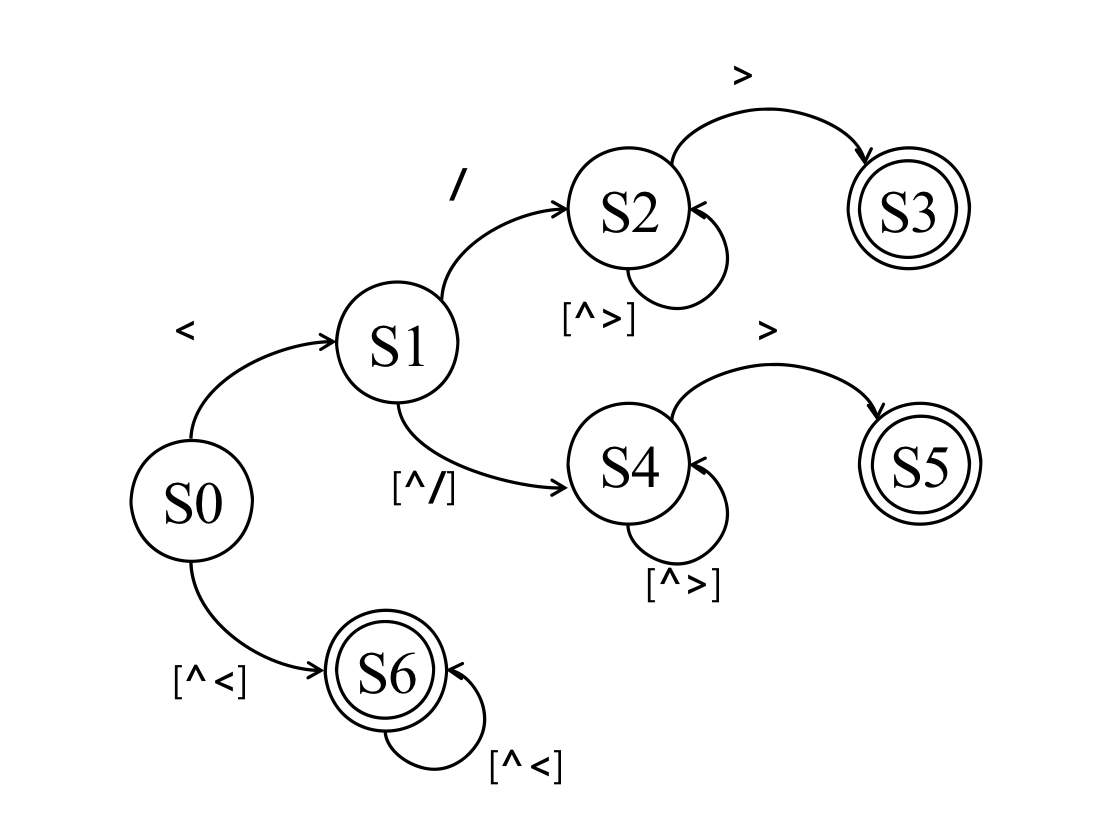
A Finite State Machine description of the specification is shown in Figure 2. Unspecified transitions from S3, S5 and S6 behave as transitions from initial state S0. The state S5 recognizes StartTag, S3 recognizes EndTag and S6 recognizes Content.
Figure 2. Finite state machine description of a HTML lexical analyzer
Lexical analysis is inherently sequential processing in that the current state is based on the previous state. However, we observe that HTML lexers converge to a stable, recurring state usually after a small number of characters. In figure 2, most of characters stay at state S6. This allows us to speculate the execution of the HTML lexer.
The steps involved are explained as below:
- Task creation and predicate generation
Given a long HTML document as input, divide it into N equal sized chunks. Make sure the chunks are overlapping and the overlap is k characters (k is of the order of 10 characters). The predicate here is a match between the state of the FSM in the overlap between chunk i and chunk i+1 (i=1…N-1).
- Mechanisms to check if the predicate is true/false
Once chunk i finishes execution, check to see if chunk i-1 has finished execution. Then check the state of the last of the overlapping characters. Since we are dealing with a Finite State Machine, the rest of the computation performed in the chunk must be correct, as it is only a function of the current state and the input. In fact, if any of the characters in the overlap are in the same state in both the chunks, there is a match. Hence, it is sufficient to just check the last character for a match.
- Commit/recovery mechanism
If the predicate for chunk i turns out to be true, then we can commit the first k characters of the chunk from i-1 and the rest from i, provided none of the predicates for chunks less than i have been invalidated. If any of them get invalidated, then restart the computation for all the invalidated blocks from the last character of the k-character overlap (whose state information is known). The rest of the chunks that have not been invalidated, but have not yet been committed (tasks that are descendents of an invalidated task), should wait until its parent is committed. Steps 2 and 3 must be repeated till chunk N can be committed.
Known uses
Speech Recognition
Speech Recognition is done using Hidden Markov Models [2] for phonemes (units of speech). Speech decoding (Converting speech to text) involves dynamic programming in the form of Viterbi Algorithm to find the most optimal sequence of words that produced the particular segment of speech data. The algorithm works iteratively. In each iteration, the algorithm looks at speech features extracted over a small window of the waveform and based on the most likely interpretations of the past sequence of inputs, tries to find the most likely states including current input. A particular traversal through the states gives a specific interpretation of the speech data as text.
In this application, the set of active states changes from iteration to iteration, according to the input waveforms. However, the set of active states has significant overlap across iterations (due to prolonged pronunciations, the phone state stays active over multiple iterations). One can speculatively compute input likelihoods for multiple iterations based on one set of the active states, to reuse the speech models associated with each active state across multiple iterations. From iteration to iteration, up to 80% of the states stays active. The states that were not speculatively computed can be computed when they become active.
Speculative task creation – For an iteration where we compute the input likelihood information, we speculatively compute the active states not just for one iteration, but for several iterations.
Predicates – The active state stays active for the next iterations
Predicate validity – The active sequence likelihood is more likely than a pruning threshold.
Recovery – If predicates are invalid, we have just done redundant work (No fixing up is required).
This is also a general speculative pattern for software cache filling algorithms that do unnecessary/redundant work.
Related Patterns
Upper level
Finite State Machine (FSM) – Finite State Machine is a good source of problems on which speculation might apply. Parsing, Lexical analysis etc are primarily written as FSM algorithms, and can use speculation to increase concurrency in the application.
Backtrack Branch & Bound (BBB) – This pattern is similar to speculation. If there is a binary decision to be made, BBB will create two tasks to explore both branches whereas speculation will “guess” and execute one of the branches. If the assumption for taking that branch is invalidated later, speculation will explore the other branch. BBB however, takes decisions based on computed bounds, rather than as guesses.
Event based implicit invocation – This is a structural pattern that is suited for an interrupt-based predicate checking using speculation. Predicates can “register” as events and the corresponding speculative tasks can be called when information related to the predicates becomes available.
Same level
Task parallelism – This is a generic pattern for handling concurrent tasks executing simultaneously on parallel hardware. It is helpful for efficient implementation and optimizations associated with speculatively executing tasks.
Lower level
Master-Worker – This pattern can be used in conjunction with speculation as an implementation strategy. We can implement some speculation instances with one thread (Master), which does all the speculation and other threads (Workers), which perform the execution of the tasks. The master thread is then responsible for task creation, predicate generation, predicate checking and task termination.
Task Queue – This implementation pattern can be used with speculation. By having a task queue that supports predicative termination, we can exploit the advantages of a parallel algorithm strategy based on speculation.
Thread Pool – This execution pattern can be used with speculation. By having a pool of threads ready, we can use them to execute the speculative tasks. This is best used with a master-worker or a task queue pattern for implementation.
Transactional Memory – This execution pattern can be used for efficient commit/recovery mechanisms with speculation.
Speculative execution – This is a similar pattern but usually fine grained and handled by the hardware (program agnostic)
References
[1] Christopher Grant Jones, Rose Liu, Leo Meyerovich, Krste Asanovic, Rastislav Bodik, “Parallelizing the Web Browser”, First USENIX workshop on Hot Topics in Parallelism (HotPar) April 2009.
[2] Lawrence R. Rabiner,”A tutorial on Hidden Markov Models and selected applications in speech recognition”. Proceedings of the IEEE, Vol. 77 (2), pp. 257-286 February 1989.
Authors
Narayanan Sundaram