Contents
Problem
Suppose a computational pattern can be decomposed into groups of semi-independent tasks interacting in an irregular fashion. The interaction is determined by the flow of data between them which implies ordering constraints between the tasks. How can these tasks and their interaction be implemented so they can execute concurrently?
Context
Some problems are most naturally represented as a collection of semi-independent entities interacting in an irregular way. What this means is perhaps clearest if we compare this pattern with the Pipeline pattern. In the Pipeline pattern, the entities form a linear pipeline, each entity interacts only with the entities to either side, the flow of data is one-way, and interaction occurs at fairly regular and predictable intervals. In the Discrete Event pattern, in contrast, there is no restriction to a linear structure, no restriction that the flow of data be one-way, and the interaction takes place at irregular and sometimes unpredictable intervals.
Also, it is sometimes desirable to compose existing, possibly sequential, program components that interact in possibly irregular ways into a parallel program without changing the internals of the components.
For problems such as this, it might make sense to base a parallel algorithm on defining a task (or a group of tightly coupled tasks) for each component, or in the case of discrete-event simulation, simulation entity. Interaction between these tasks is then based on the ordering constraints determined by the flow of data between them.
Forces
A good solution should make it simple to express the ordering constraints, which can be numerous and irregular and even arise dynamically. It should also make it possible for as many activities as possible to be performed concurrently.
Ordering constraints implied by the data dependencies can be expressed by encoding them into the program (for example, via sequential composition) or using shared variables, but neither approach leads to solutions that are simple, capable of expressing complex constraints, and easy to understand.
Solution
A good solution is based on expressing the data flow using abstractions called events, with each event having a task that generates it and a task that processes it. Because an event must be generated before it can be processed, events also define ordering constraints between the tasks. Computation within each task consists of processing events.
Defining the tasks
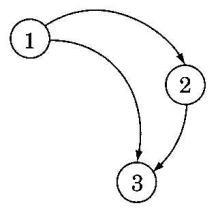
The basic structure of each task consists of receiving an event, processing it, and possibly generating events, as shown in Figure 1.
If the program is being built from existing components, the task will serve as an instance of the Facade pattern [GHJV95] by providing a consistent event-based interface to the component.
The order in which tasks receive events must be consistent with the application’s ordering constraints, as discussed later.
Figure 1. Basic structure of a task in the Discrete Event pattern
Representing event flow
To allow communication and computation to overlap, one generally needs a form of asynchronous communication of events in which a task can create (send) an event and then continue without waiting for the recipient to receive it. In a message-passing environment, an event can be represented by a message sent asynchronously from the task generating the event to the task that is to process it. In a shared-memory environment, a queue can be used to simulate message passing. Because each such queue will be accessed by more than one task, it must be implemented in a way that allows safe concurrent access, as described in the Shared Queue pattern. Other communication abstractions, such as tuple spaces as found in the Linda coordination language or JavaSpaces [LFHA99], can also be used effectively with this pattern. Linda [CG91] is a simple language consisting of only six operations that read and write an associative (that is, content-addressable) shared memory called a tuple space. A
tuple space is a conceptually shared repository for data containing objects called tuples that tasks use for communication in a distributed system.
Enforcing event ordering
The enforcement of ordering constraints may make it necessary for a task to process events in a different order from the order in which they are sent, or to wait to process an event until some other event from a given task has been received, so it is usually necessary to be able to look ahead in the queue or message buffer and remove elements out of order. For example, consider the situation in Figure 2. Task 1 generates an event and sends it to task 2, which will process it, and also sends it to task 3, which is recording information about all events. Task 2 processes the event from task 1 and generates a new event, a copy of which is also sent to task 3. Suppose that the vagaries of the scheduling and underlying communication layer cause the event from task 2 to arrive before the event from task 1. Depending on what task 3 is doing with the events, this may or may not be problematic. If task 3 is simply tallying the number of events that occur, there is no problem. If task 3 is writing a log entry that should reflect the order in which events are handled, however, simply processing events in the order in which they arrive would in this case produce an incorrect result. If task 3 is controlling a gate, and the event from task 1 results in opening the gate and the event from task 2 in closing the gate, then the out-of-order messages could cause significant problems, and task 3 should not process the first event until after the event from task 1 has arrived and been processed.
Figure 2. Event-based communication among three tasks. Task 2 generates its event in response to the event received from task 1. The two events sent to task 3 can arrive in either order.
In discrete-event simulations, a similar problem can occur because of the semantics of the application domain. An event arrives at a station (task) along with a simulation time when it should be scheduled. An event can arrive at a station before other events with earlier simulation times.
The first step is to determine whether, in a particular situation, out-of-order events can be a problem. There will be no problem if the “event” path is linear so that no out-of- order events will occur, or if, according to the application semantics, out-of-order events do not matter. If out-of-order events may be a problem, then either an optimistic or pessimistic approach can be chosen. An optimistic approach requires the ability to roll back the effects of events that are mistakenly executed (including the effects of any new events that have been created by the out-of-order execution). In the area of distributed simulation, this approach is called time warp [Jef85]. Optimistic approaches are usually not feasible if an event causes interaction with the outside world. Pessimistic approaches ensure that the events are always executed in order at the expense of increased latency and communication overhead. Pessimistic approaches do not execute events until it cau be guaranteed “safe” to do so. In the figure, for example, task 3 cannot process an event from task 2 until it “knows” that no earlier event will arrive from task 1 and vice versa. Providing task 3 with that knowledge may require introducing null events that contain no information useful for anything except the event ordering. Many implementations of pessimistic approaches are based on time stamps that are consistent with the causality in the system [Lam78].
Much research and development effort has gone into frameworks that take care of the details of event ordering in discrete-event simulation for both optimistic [RMC+98] and pessimistic approaches [CLL+99]. Similarly, middleware is available that handles event-ordering problems in process groups caused by the communication system. An example is the Ensemble system developed at Cornell [vRBH+98].
Avoiding deadlocks
It is possible for systems using this pattern to deadlock at the application level—for some reason the system arrives in a state where no task can proceed without first receiving an event from another task that will never arrive. This can happen because of a programming error; in the case of a simulation, it can also be caused by problems in the model that is being simulated. In the latter case, the developer must rethink the solution.
If pessimistic techniques are used to control the order in which events are processed, then deadlocks can occur when an event is available and actually could be processed, but is not processed because the event is not yet known to be safe. The deadlock can be broken by exchanging enough information that the event can be safely processed. This is a very significant problem as the overhead of dealing with deadlocks can cancel the benefits of parallelism and make the parallel algorithms slower than a sequential simulation. Approaches to dealing with this type of deadlock range from sending frequent enough “null messages” to avoid deadlocks altogether (at the cost of many extra messages) to using deadlock detection schemes to detect the presence of a deadlock and then resolve it (at the cost of possible significant idle time before the deadlock is detected and resolved). The approach of choice will depend on the frequency of deadlock. A middle-ground solution is to use timeouts instead of accurate deadlock detection, and is often the best approach.
Scheduling and processor allocation
The most straightforward approach is to allocate one task per PE and allow all the tasks to execute concurrently. If insufficient PEs are available to do this, then multiple tasks can be allocated to each PE. This should be done in a way that achieves good load balance. Load balancing is a difficult problem in this pattern due to its potentially irregular structure and possible dynamic nature. Some infrastructures that support this pattern allow task migration so that the load can be balanced dynamically at runtime.
Efficient communication of events
If the application is to perform well, the mechanism used to communicate events must be as efficient as is feasible. In a shared-memory environment, this means making sure the mechanism does not have the potential to become a bottleneck. In a message- passing environment, there are several efficiency considerations; for example, whether it makes sense to send many short messages between tasks or try to combine them. [YWC96] and [WY95] describe some considerations and solutions.
Invariants
– No event will have an effect on the system out of order.
Examples
As a real-world analogy, consider a newsroom, with reporters, editors, fact- checkers, and other employees collaborating on stories. As reporters finish stories, they send them to the appropriate editors; an editor can decide to send the story to a fact-checker (who would then eventually send it back) or back to the reporter for further revision. Each employee is a semi-independent entity, and their interaction (for example, a reporter sending a story to an editor) is irregular.
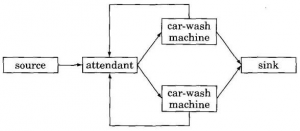
Many other examples can be found in the field of discrete-event simulation, that is, simulation of a physical system consisting of a collection of objects whose interaction is represented by a sequence of discrete “events”. An example of such a system is the car-wash facility described in [Mis86]: The facility has two car-wash machines and an attendant. Cars arrive at random times at the attendant. Each car is directed by the attendant to a non-busy car-wash machine if one exists, or queued if both machines are busy. Each car-wash machine processes one car at a time. The goal is to compute, for a given distribution or arrival times, the average time a car spends in the system (time being washed plus any time waiting for a non-busy machine) and the average length of the queue that builds up at the attendant. The “events” in this system include cars arriving at the attendant, cars being directed to the car-wash machines, and cars leaving the machines. Figure 3 sketches this example. Notice that it includes “source” and “sink” objects to make it easier to model cars arriving and leaving the facility. Notice also that the attendant must be notified when cars leave the car-wash machines so that it knows whether the machines are busy.
Fig 3. Discrete-event simulation of a car-wash facility. Arrows indicate the flow of events.
TODO: A fully worked-out and detailed pedagogical example
Known Uses
A number of discrete-event simulation applications use this pattern. The DPAT simulation used to analyze air traffic control systems [WieOl] is a successful simulation that uses optimistic techniques. It is implemented using the GTW (Georgia Tech Time Warp) System [DFP94]. The paper ([WieOl]) describes application-specific tuning and several general techniques that allow the simulation to work well without excessive overhead for the optimistic synchronization. The Synchronous Parallel Environment for Emulation and Discrete-Event Simulation (SPEEDES) [Met] is another optimistic simulation engine that has been used for large-scale war-gaming exercises. The Scalable Simulation Framework (SSF) [CLL99] is a simulation framework with pessimistic synchronization that has been used for large-scale modeling of the Internet.
The CSWEB application described in [YWC96] simulates the voltage output of combinational digital circuits (that is, circuits without feedback paths). The circuit is partitioned into sub-circuits; associated with each are input signal ports and output voltage ports, which are connected to form a representation of the whole circuit. The simulation of each sub-circuit proceeds in a time-stepped fashion; at each time step, the sub-circuit’s behavior depends on its previous state and the values read at its input ports (which correspond to values at the corresponding output ports of other sub- circuits at previous time steps). Simulation of these sub-circuits can proceed concurrently, with ordering constraints imposed by the relationship between values generated for output ports and values read on input ports. The solution described in [YWC96] fits the Discrete Event pattern, defining a task for each sub-circuit and representing the ordering constraints as events.
Ptolemy II is a actor-based framework that allows experimentation on multiple Models of Computation. One of the models of computations it considers is Discrete Event (DE), and it provides a environment in which users can develop new actors or create applications based on existing actors. Furthermore it provides extended versions of DE where it is implemented in a distributed form (DDE), and explores the tradeoffs described above.
Related Patterns
This pattern is similar to the Pipeline pattern in that both patterns apply to problems in which it is natural to decompose the computation into a collection of semi- independent entities interacting in terms of a flow of data. There are two key differences. First, in the Pipeline pattern, the interaction among entities is fairly regular, with all stages of the pipeline proceeding in a loosely synchronous way, whereas in the Discrete Event pattern there is no such requirement, and the entities can interact in very irregular and asynchronous ways. Second, in the Pipeline pattern, the overall structure (number of tasks and their interaction) is usually fixed, whereas in the Discrete Event pattern, the problem structure can be more dynamic.
This pattern should not be confused with the “Event-based, implicit invocation” structural pattern, which mainly provides architecture guidance for the application, while this one provides a strategy for parallel implementation of a given computational pattern.
References
[GHJV95]
[LFHA99]
[CG91]
[Jef85]
[Lam78]
[RMC+98]
[CLL+99]
[vRBH+98]
[YWC96]
[WY95]
[Mis86]
[WieOl]
[DFP94]
[Met]