Contents
Problem
We often describe a problem as a collection of tasks operating on data. When many of the tasks can be executed concurrently, how can we efficiently exploit the concurrency?
Context
In the compute-centric view of a problem, we focus on defining a set of tasks that operates on data. The underlying assumption is that the problem is compute-intensive and the distribution of data working set is of secondary concern for performance. This assumption is often valid for systems with a shared memory space, where concurrently executing tasks have small working sets and infrequent access to shared global data structures. In the case where distribution of data is crucial for execution efficiency, we should use the Data Parallel Algorithm Strategy Pattern, where the problem is expressed in terms of a single stream of tasks applied to each independent element of a data structure, and the solution involves efficient execution of tasks with data distribution as a primary concern.
The set of tasks for a problem can be derived from the structure pattern or computation pattern that describes the problem. For example:
-
In the Agent and Repository Structural Pattern, where the problem is expressed in terms of a collection of independent tasks (i.e. autonomous agents) operating on a large data set (i.e. a central repository), and the solution involves efficiently managing all accesses by the agents while maintaining data consistency, a task can be the execution of an agent, or the operation where each agent is updating the repository.
-
In the Graph Algorithm Computation Pattern, where the problem is expressed in terms of vertices and edges in a graph, and the solution involves efficient analysis and manipulation of the graph, a task can be the evaluation of at a vertex or over an edge, or the traversal of a path starting from a vertices. One application that uses this pattern is large vocabulary continuous speech recognition.
For many problems, there is more than one way to define a task. For example, in the Monte Carlo Methods Computation Pattern, where the problem is expressed in terms of statistical sampling of solution space with experiments using different parameter settings, and the solution involves the efficient construction and execution of experiments and efficient analysis of the results to arrive at a solution, a task can be the execution of a set of experiments, a single experiment, or concurrent steps within an experiments. One application is in Value-at-Risk analysis in Computational Finance.
Tasks can be independent, or they can share data and collaborate. For example, in the Dynamic Programming Computation Pattern, where the problem is expressed in terms of natural optimal substructures where by optimally solving a sequence of local problems, one can arrive at a globally optimal solution, and the solution involves efficient construction and execution of local problems and assembling them to arrive at the global optimal solution, a task can be independent sub-problem, sub-problems that share data with other sub-problems.
Tasks can be known at beginning of execution, or can be generated as the computation unfolds. For example, in Backtrack Branch and Bound Computation Pattern, where the problem is expressed in terms of searching a solution space to make a decision or find an optimal solution, and the solution involves dividing the search space into sub-spaces and efficiently bound and prune the search spaces, a task can be the evaluation of sub-spaces, which are generated dynamically during the branch and bounding process.
For most types of problems, all task usually need to be completed to solve the problem. In some types of problems such as Backtrack Branch and Bound, an optimal solution can be reached before all tasks are completed.
Forces
Task granularity: we want to generate greater number of smaller tasks so there is more opportunities for load balance, but greater number of tasks incur more management overhead; we can generate smaller number of larger tasks which would reduce management overhead, at the expense of less opportunities for load balancing.
Task interaction: we can duplicate computation in tasks to minimize the interactions between task to reduce task synchronization overhead, we can also minimize computation duplication at the expense of more synchronization between tasks. Examples of this trade-off can be found in Dynamic Programming Computation Pattern and Backtrack Branch and Bound Computation Pattern.
Solution
The solution can arrived at in three steps:
-
Understanding application concurrency characteristics
-
Understanding implementation platform characteristics
-
Using a flexible Parallel Algorithm Strategy Pattern to map structural and computation patterns onto implementation strategy patterns
Depending on usage scenarios, one may iterate between step 1 and step 2. For example, one may pick an the implementation platform, then evaluate whether the application can be efficiently mapped to the platform, or one may expose all levels of parallelism, and then pick an implementation platform to construct the application. In some cases, the application may have different components that will be implemented on different platforms.
1. Understanding application concurrency characteristics
It is important to understand the range of granularities a problem has to see how it can be best mapped to an implementation platform. Some applications may have a wide range of granularities, some have a much smaller range.
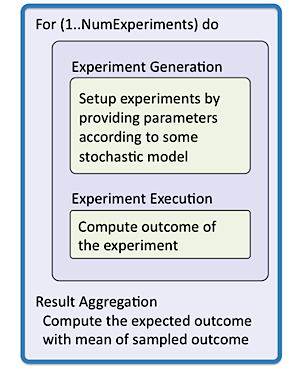
The problems in Monte Carlo Simulation Computation Pattern has a wide range of possible granularities. Using risk analysis in computational finance as an example: The problem aims estimate the risks in a financial contract given the volatility in future market conditions. It does the estimation by modeling the uncertainty in market conditions with a set of experiments with varying market parameters and measuring the liabilities and profits the financial contract would generate. In a typical Monte Carlo Simulation, tens of thousands to millions of experiments are conducted.
As shown in figure, there is an outer loop for conducting all experiments. A task could be defined as one experiment or an arbitrary subset of experiments, allowing efficient mapping to a wide variety of implementation platforms.
On the other hand, some problems in Graph Algorithms Computation Pattern often have a small range of possible granularities. In graph traversal for speech recognition for example, the goal is to find the most-likely sequence of word uttered by a speaker. The figure shows the architecture of a speech recognition system. The recognition process uses a recognition network, which is a language database that is compiled offline from a variety of knowledge sources using powerful statistical learning techniques. The speech feature extractor collects discriminant feature vectors from input audio waveforms, and then the inference engine computes the most likely word sequence based on the extracted speech features and the recognition network.
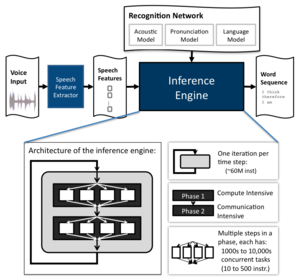 A parallel inference engine traverses a graph-based knowledge network consisting of millions of states and arcs. As shown in the figure, it uses the Viterbi search algorithm to iterate through a sequence of input audio feature one time step at a time. The Viterbi search algorithm keeps track of each alternative interpretation of the input utterance as a sequence of states ending in an active state at the current time step. It evaluates out-going arcs based on the current-time-step observation to arrive at the set of active states for the next time step. The traversal is heavily pruned, keeping track of on average 0.1-1.0% of the total state space. Each time step consists of two phases: Phase 1 – observation probability computation and Phase 2 – arc transition computation. Phase 1 is compute intensive while Phase 2 is communication intensive.
A parallel inference engine traverses a graph-based knowledge network consisting of millions of states and arcs. As shown in the figure, it uses the Viterbi search algorithm to iterate through a sequence of input audio feature one time step at a time. The Viterbi search algorithm keeps track of each alternative interpretation of the input utterance as a sequence of states ending in an active state at the current time step. It evaluates out-going arcs based on the current-time-step observation to arrive at the set of active states for the next time step. The traversal is heavily pruned, keeping track of on average 0.1-1.0% of the total state space. Each time step consists of two phases: Phase 1 – observation probability computation and Phase 2 – arc transition computation. Phase 1 is compute intensive while Phase 2 is communication intensive.
There exist significant application concurrency in each steps within the phases of execution of the inference engine, we can evaluate thousands of alternative interpretations of a speech utterance concurrently. However, the algorithm requires frequent synchronizations between steps in these phases of execution, limiting the scope of the task level parallelism. Specifically, with tens to hundreds of instructions per task, and a few thousands of tasks per step, these fine-grained concurrency can only be exploited with software or hardware level task queue based implementation platforms.
2. Understanding implementation platform characteristics
For efficient exploitation of the problem concurrency, we must consider the following two factors in task parallelism algorithm strategy:
-
How to define the task granularity?
-
How to trade-off synchronization verses computation duplication?
Efficient implementations often require extensive knowledge of the platform characteristics. Efficient task granularity is dependent on the task management overhead of an implementation platform, and an optimal trade-off for the amount of task interactions to use in the application depends on the synchronization overhead of an implementation platform with respect to its compute capabilities.
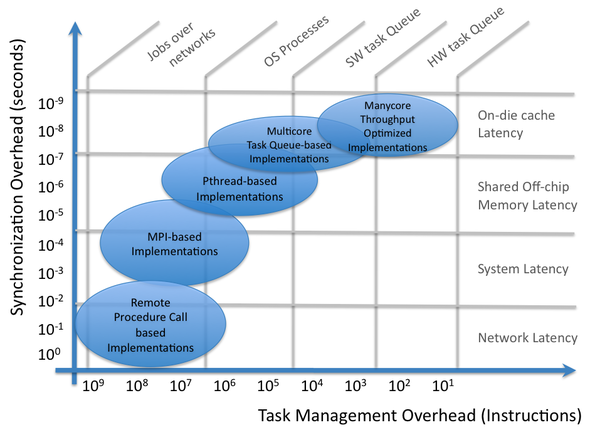
Table 1 illustrates the range of task management overheads for various parallel implementation platforms. The higher level task management mechanisms have significantly larger overheads, which only makes sense to use for large enough task granularities, but also provide services such as failover-resubmit functions. The lower level task management mechanisms have minimal overheads that allow fine-grained parallelism to be exploited, at the expense of having limited functions and services.
Table 1. Task Management Overheads and Implications
| Task Management Mechanism | Overhead of Task Management | Efficient Task Size | Service Provided |
|---|---|---|---|
| Jobs over Networks | 100-1000 ms | 10M+ instructions | Failover protection |
| OS Processes | 100-1000 ns | 10k-10M instructions | Task preemption and resume |
| SW Task Queue | 10-100 ns | 100-10k instructions | Abort remaining tasks |
| HW Task Queue | 1-10 ns | 10-1000 instructions | All task execute to completion |
Table 2 illustrates the range of synchronization overheads for parallel implementation platforms. Synchronization over networks and disks require significant overhead in the range of 100s ms, but provide Tera Byte and Peta Byte level working set. Synchronization over on-chip cache provide ns-scale overhead at the expense of having only KB to MB range working set.
Table 2. Synchronization Overheads and Implications
| Synchronization Mechanism | Overhead of Synchronization | Data Working Set |
|---|---|---|
| Over Networks / Disks | 100-1000 ms | TB or more |
| Over Fast Buses | 100-1000 us | 10-100 GB |
| Shared Off-chip Memory | 100-1000 ns | 10-40 GB |
| Shared On-chip Last Level Cache | 10-100 ns | 1-20 MB |
| Shared On-chip L1 Cache | 1 ns | 10 KB |
Figure 1 illustrates the common ranges of implementation platform capabilities, and provide a guideline to the task management overheads and data synchronization overheads one has to work with. As more compute capabilities are being concentrated on-chip, we see the emergence of SW Task Queue and HW Task Queue based implementation platforms being increasingly important to support fine-grained application concurrency.
3. Flexibly Mapping the Task Parallelism
Once we understand the application concurrency characteristics, it restricts the range of implementation platforms suitable for exploiting the application concurrency. In some cases, such as with the Monte Carlo Simulation based applications, the application has significant range of flexibilities in terms of the task granularity.
There exist patterns for flexibly determining the task granularity suitable for an implementation platform. In the Recursive Splitting Algorithm Strategy Pattern, the problem is expressed in terms of the composition of a series of tasks that are generated recursively, and the solution involves recursively splitting work into fine-enough granularities for effective load balancing.
There are also other alternatives to load balance a parallel implementation platform. In Task Queue Implementation Strategy Pattern, the problem is expressed in terms of a list of tasks that can be executed in parallel, and the solution involves having an efficient way to load balance the system without having the task queue becoming performance bottleneck.
Invariants
Tasks must have finite execution times
Example
Monte Carlo Simulations on a Cluster of Computers
We illustrate the task parallelism pattern using Monte Carlo Simulation on Multicore processors as an example to illustrate the definition of task granularity and the interactions between tasks.
Understanding application concurrency characteristics
One scenario where Monte Carlo Simulation is used is in risk management in a financial firm. The risks a financial firm assumes are in the form of financial contracts it enters given the volatility in future market conditions. The risk is usually measured by a metric called Value-at-Risk (VaR). For example, if a portfolio of stocks has a one-day 5% VaR of $1 million, there is a 5% probability that the portfolio will fall in value by more than $1 million over a one day period, assuming markets are normal and there is no trading. Informally said, one should expect a loss of $1 million or more on this portfolio ion 1 out of 20 days. However, as long as there is a large expected long term gain, the risk may be justified.
A large financial firm can have as many as 500,000 contracts in any given day, in the form of various forms of options and financial trading instruments. Each contract should have its risks evaluated based on its terms and conditions given new market information collected each day. Based on the risk profile of each contract, the firm may decide to buy or sell the contracts to adjust its portfolio‘s exposure to market volatility.
To evaluate the risk of a contract, one typically sample 1000 market scenarios, each over 30 to 100 time steps. This provides multiple levels of potential concurrency in the application to map to a parallel implementation platform. At the top level, all 500,000 contacts can be evaluated independently. For each contract, the 1000 market scenarios can be evaluated independently. For each scenario, the uniformly distributed (pseudo) random number generation can be generated independently; scenario generation requires some sequential processing, and scenario evaluation over the time steps happens sequentially.
Understanding implementation platform characteristics
On the implementation platform side: a typical implementation platform such as one that is based on Intel Core i7 architecture has several levels of parallelism. There is the SIMD level parallelism within a thread, multiple threads sharing a core, multiple cores on a chip in a system, and multiple system in a cluster.
The SIMD level is the most restrictive parallelism to take advantage of, where instructions must execute in lock step on a processor pipeline cycle-to-cycle basis. This has implications on what level of concurrency can be uniform enough to be mapped to this level. For the multiple threads sharing a core, the threads not only share the computation resources but also share the resources in the memory sub-system. This has implications on the amount of parallelism to expose, and care must be taken to take advantage of local data reuse, and not to expose too much parallelism to overwhelm the memory subsystem. Cores on the same chip share chip-level resources, and has also has the same resource constraints to consider. Across systems in a cluster, systems are loosely coupled, and communication between clusters machines is expensive.
Flexibly mapping the task parallelism
Given the application concurrency and the platform parallelism, we can make the following mapping:
Map scenarios to SIMD lanes: different scenarios of the same instruments are usually simulated with the same routines, thus simulation in lock step is not a significant constraint. The task granularity can be controlled by mapping multiple scenario at a time to one task, such that the scenarios are simulated sequentially to increase the task granularity and reduce task management overhead.
Map scenarios to threads on a core: Mapping different scenarios of the same instruments onto different threads of the same core, there are instrument specific parameters that could be shared in the memory hierarchy within a core that will reduce overhead, also the results of the different scenarios can be aggregated within the same memory hierarchy, increasing task to task interaction efficiency, reducing the communication overhead.
Map contracts to cores: Contracts are independent and can be mapped to different cores. The aggregated risks can be summarized on a per core basis.
Map contracts to systems in a cluster: Contracts are independent and can be mapped to different cores. The final risk aggregation can occur with the cluster-wide reduction at the end of the risk analysis computation.
Known uses
Thread Building Block (TBB): TBB from Intel Corp is an implementation infrastructure that follows an Recursive Splitting Algorithm Strategy Pattern that finds an optimal task granularity.
Compute Device Unified Architecture (CUDA): CUDA from NVIDIA is an implementation infrastructure with fine implementation task granularity that uses a Hardware based Task Queue implementation.
Related patterns
Patterns that uses Task Parallelism Algorithm Strategy:
-
Agent and Repository Structural Pattern
-
Graph Algorithm Computation Pattern
-
Monte Carlo Methods Computation Pattern
-
Dynamic Programming Computation Pattern
-
Graph Algorithm Computation Pattern
-
Backtrack Branch and Bound Computation Pattern
Related Algorithm Strategies:
-
Data Parallel Algorithm Strategy Pattern
Patterns that Task Parallelism Algorithm Strategy uses:
-
SPMD Implementation Strategy Pattern
-
Fork/Join Implementation Strategy Pattern
-
Master/Worker Implementation Strategy Pattern
-
Loop Parallelism Implementation Strategy Pattern
-
Task Queue Implementation Strategy Pattern
References
-
Timothy G Mattson, Beverly A Sanders, Berna L. Massingill, “Patterns for Parallel Programming”, Addison Wesley, 2004.
Author
Jike Chong (Shepherd: Youngmin Yi)