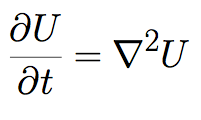Geometric Decomposition

How can an algorithm be organized around a data structure that has been decomposed into concurrently updatable “chunks” ?

Many important problems are best understood as a sequence of operations on a core data structure. There may be other work in the computation, ut an effective understanding of the full computation can be obtained by understanding how the core data structures are updated. For these types of problems, often the best way to represent the concurrency is in terms of decompositions of these core data structures. (This form of concurrency is sometimes known as domain decomposition, or coarse-grained data parallelism.)

The way these data structures are built is fundamental to the algorithm. If the data structure is recursive, any analysis of the concurrency must take this recursion into account. For recursive data structures, the Recursive Data and Divide and Conquer patterns are likely candidates. For arrays and other linear data structures, we can often reduce the problem to potentially concurrent components by decomposing the data structure into contiguous substructures, in a manner analogous to dividing a geometric region into subregions – hence the name Geometric Decomposition. For arrays, this decomposition is along one or more dimensions, and the resulting subarrays are usually called blocks. We will use the term chunks for the substructures or subregions to allow for the possibility of more general data structures, such as graphs.

This decomposition of data into chunks then implies a decomposition of the update operations into tasks. Each task represents the update of one chunk, and tasks execute concurrently. If each task can be executed with information entirely local to its chunk, then the concurrency is embarassingly parallel and the Task Parallelism pattern should be used. In many cases, however, the update requires information from points in other chunks (frequently from what we can call neighboring chunks – chunks containing data that was nearby in the original global data structure). In these cases, information must be shared between chunks to complete the update.

• Locality – the decomposition respects the re-use patterns inherent in a computation.

• load-balance – all processors have a roughly equal amount of work to do. Load balance is always a concern when the data structure is irregular (e.g. a graph or a sparse matrix), but can also be important for regular data structures (e.g. dense arrays and matrices).

• We must ensure the data required for each chunk update is present when needed. This is analogous to managing data dependencies in the Task Parallelism pattern.

Designs for problems that fit this pattern involve the following key elements: Data Decomposition: Partitioning the global data structure into chunks,Data Exchange: ensuring that each task has access to all the data it needs to perform the update operation for its chunk, Update Operation: performing the update to local data, Data Distribution and Task Schedule: mapping chunks to UEs in a way that gives good performance.

The granularity of the data decomposition has a significant impact on the effciency of the program. In a coarse-grained decomposition, there are a smaller number of large chunks.

On a distributed-memory machine, the chunk size usually correlates with the size of messages that need to be exchanged between nodes. When chunks, and therefore messages, are large, network transfers are more efficient, as the message-passing overheads are amortized over the size of the message.

On a shared-memory machines, however, the cost of synchronization and communication is in general much smaller. Instead, domain-decomposition decisions should be made based on the memory access patterns they produce. While on a distributed-memory system, each node has a separate data structure representing its local chunk, shared-memory decompositions frequently result in simultaneous accesses by multiple UEs. Thus it is difficult to decouple the domain decomposition from memory access optimizations. For example, consider a geometric decomposition of a row-major 2-Dimensional array. It will usually be beneficial for chunks to consist of contiguous groups of rows; within a chunk, a UE can access memory in a unit-stride pattern. As discussed in the Cache Blocking pattern, such accesses are very efficient.

It may be possible in some cases to derive an optimal granularity by manually analyzing the program. In practice, however, the complexity of the interactions between programs and hardware necessitates experimentation with different decomposition strategies. Programs should be implemented so that decomposition granularities are parameters, either at compile-time or at runtime, so that a programmer can empirically determine the best size for a given target platform.

The shape of the chunks can also affect the amount of data shared between tasks. On distributed-memory machines data-sharing requires communication, which is usually very expensive. On shared-memory machines, data-sharing requires multiple UEs to load data from DRAM into caches. Multiple UEs loading the same data is effectively a waste of DRAM bandwidth, a resource which is frequently under heavy contention on single-socket parallel processors. For both shared and distributed memory systems, the amount of data shared frequently correlates with the amount of “surface area” that two chunks share – i.e. the boundaries between chunks. Because the computation scales with the number of points within a chunk, it scales as the volume of the region. The surface-to-volume effect can be exploited to minimize data sharing, frequently by dividing in multiple dimensions.

Consider the row-major NxN 2D array being shared by 4 UEs. Dividing the array into four chunks of contiguous rows – i.e. four sub-arrays of size Nx(N/4). The two “inner” processors’ chunks have boundary areas of 2N, while the two “outer” processors’ chunks have boundary areas of N – a total surface area of 6N. If instead the array is decomposed into four square chunks of size (N/2)x(N/2), all four chunks’ boundaries have area (N/2) + (N/2), and the total shared surface area of the decomposition is 4N.

In some cases, the preferred shape of the decomposition can be dictated by other concerns: frequently, data decomposition decisions must balance performance against the desire to re-use existing code and the need to interface with other steps in the computation. It may be the case, for example, that existing sequential code can be more easily reused with a lower-dimensional decomposition, and the potential increase in performance is not worth the effort of reworking the code. Also, an instance of this pattern can be used as a sequential step in a larger computation. If the decomposition used in an adjacent step is different, it may not be worthwhile. In distributed-memory systems, switching domain decompositions can require significant communication overhead. On shared-memory machines, it may require data-structure reorganization – a class of operations which are unlikely to exhibit good memory-access performance, as they require UEs to access one datastructure in the sequence for which the second datastructure is optimized.

An effective technique for managing data-sharing and communication due to domain-decomposition is to replicate the necessary non-local data. Consider our example of the row-major 2D array, using the column-wise chunk decomposition. If each element’s computation requires the nearest neighbor in each of the East and West directions, then each chunk could be padded with an extra column on either side in which to store the elements owned by other UEs. While this technique is more applicable in distributed-memory machines, it is also useful in shared memory machines in the presence of software-managed local memories. The extra “padding” is usually referred to as ghost cells or a ghost boundary. Ghost cells provide two benefits: on distributed-memory systems, their use enables the consolidation of communication into fewer, larger messages. Second, the communication of ghost cells can be overlapped with the update of the interior of the arrays which do not depend on the ghost cells. Thus communication costs can be hidden by computation.

A key factor in using this pattern correctly is ensuring that nonlocal data required for the update operation is obtained before it is needed.

If all the data needed is present before the beginning of the update operation, the simplest approach is to perform the entire exchange before beginning the update, storing the required nonlocal data in a local data strcuture designed for that purpose. This approach is straightforward to implement using either copying (on shared-memory machines) or message passing (on distributed-memory machines).

More sophisticated approaches which overlap communication with computation are also possible. Such approaches are necessary if some data for the update is not initially available, and may improve performance in other cases. On platforms where communication and computation occur in parallel, the savings from such an approach can be significant. For distributed memory machines, standard communication libraries include classes of non-blocking message passing routines. On hardware-multi-threaded shared memory machines, a program may also simply utilize the latency-hiding provided by the hardware thread switching. However, in some platforms, the multithreading may only be sufficient to hide L1-cache misses, rather than the longer latency of misses in higher level caches that result in DRAM accesses. The low-level details of the exchange operation’s implementation can have a large impact on efficiency. Programmers should leverage optimized implementations of communication routines, if they exist for the target system.

Updating the data structure is done by concurrently executing the tasks, each responsible for the update of one chunk of the data structure. If all the needed data is present at the beginning of the update operation, and if none of this data is modified during the course of the update, parallelization is easier and more likely to be efficient.

If the required exchange of information has been performed before beginning the update operation, the update itself is usually straightforward to implement. It is essentially identical to the analogous update in an equivalent sequential program, particularly if good choices have been made about how to represent nonlocal data. For example, if ghost cells have been made to appear simply as extensions to the local data structure, rather than as separate data structures.

If the exchange and update operations overlap, care must be taken to ensure the update is performed correctly. If a system supports lightweight threads that are well integrated with the communication system, then overlap can be achieved via multithreadig within a single task. One thread computes the update and another handles communication. In this case, synchronization between threads is required. On systems with hardware multi-threading, especially on massively-multithreaded GPUs, one may not need to explicitly orchestrate the overlap of computation and communication.

The final step in designing a parallel algorithm for a Geometrically Decomposable problem is mapping the collection of tasks, and the data corresponding to those tasks, onto UEs. Each UE then “owns” collections of chunks. Thus, we have a two-tiered scheme for data distribution: partitioning the data into chunks, then assigning these chunks to UEs. This scheme is flexible enough to represent a variety of popular schemes for distributing data among UEs.

In the simplest case, each task can be statically assigned to a separate UE; then all tasks can execute concurrently. The inter-task coordination needed to implement the exchange operation is straightforward. This approach is most appropriate when the computation times of the tasks are uniform and the exchange operation has been implemented to overlap communication and computation within each task.

The simple approach can lead to poor load balance in some situations, however, For example, consider a linear algebra problem in which elements of the matrix are successively eliminated as the computation proceeds. Early in the computation, all the rows and columns of the matrix are full; decompositions based on assigning full rows or columns to UEs are effective. Later in the computation, rows or columns become sparse, the work per row becomes uneven, and the computational load becomes poorly balanced. The solution is to decompose the problem into many more chunks than there are UEs, and to distribute the data with a cyclic or block-cyclic distribution. (discussed in the Distributed Array pattern). As chunks become sparse, there are likely other nonsparse chunks for any given UE to work on, and the load is more balanced. A rule of thumb is to produce 10 times as many tasks as UEs.

It is also possible to use dynamic load-balancing algorithms to redistribute the chunks among the UEs to improve load balance. These incur implementation and runtime overhead that must be traded off against the performance improvement of load-balancing. Generally, one should attempt a static cyclic allocation strategy first.

This example will demonstrate the Geometric Decomposition of the heat equation. For pedagogy, we will begin with a 1D formulation.

The heat equation is a partial differential equation describing the diffusion of heat throughout a volume over time:

In one dimension, the Laplacian operator is simply the second derivative with respect to the spatial dimension:

Our approach is to discretize the problem space, representing U by a 1-Dimensional array and computing values for a sequence of discrete time steps. We will only save values of U for two time steps: we will call these arrays ut (U at time step t) and utp1 (U at time step t + 1):

utp1[i] = ut[i] + (dt/(dx*dx*)) * (ut[i+1] - 2*ut[i] + uk[i-1]);

The translation from the continuous derivative to the discrete differences can be derived from the definition of the derivative; in the limit as dt and dxgo to zero, the discrete formula becomes equivalent to the continuous one. Observe that for the i^th element of utp1, only the i, i-1, and i+1 values ofut are needed – i.e. only the corresponding value in ut and its two closest neighbors.

We can design the parallel algorithm for this problem by geometrically decomposing the arrays ut and utp1 into contiguous subarrays, i.e. chunks. The updates to these chunks can be computed concurrently. Note that the computation of the values on the chunk boundaries will require data from neighboring chunks.

The overall program structure for applications of this pattern will normally use either the Loop Parallelism pattern or the SPMD pattern, with the choice determined largely by the target platform.

For data structures that are not linear or multi-dimensional arrays, decomposition requires problem-specific techniques. However, many pointer-based data-structures can be considered graphs, and techniques in the Graph Partitioning pattern may apply.

Tim Mattson, Mark Murphy