Contents
Problem
Data associated with grid elements in irregular, multi-dimensional, geometric layouts need to be updated by methods which determine new values based on other values in their physical proximity. Neighborhood relations are irregular and complex and need to be stored explicitly. How do you design a solver which provides these updates, scales too many processors, and parallelizes efficiently?
Context
Many problems involve objects with irregular geometric definitions. The datasets representing these objects are typically defined as a mesh covering the surfaces or volumes of these objects. Distances and directions between mesh points may vary depending on the local properties of the problem domain and permit a very flexible geometric description. Entities in the mesh (i.e., points, edges, faces, and/or volumes) must be explicitly represented, usually using multiple tables, one for each entity type. Relations between these entities and tables have to be stored explicitly using pointers or address lists.
Computations frequently involve the numerical solution of differential equations. Applications typically require the modeling of quantities such as tension, temperature, or pressure at each point in the grid, evolving over time. Computations typically proceed as a sequence of mesh update steps. For example, for explicit methods, at each step, values associated with each entity are updated in parallel, based on values retrieved from neighboring entities. Or for implicit methods, a sparse linear algebra problem is solved at each step. Datasets can be very large.
The following figures show examples of problem geometries with its associated unstructured meshes.
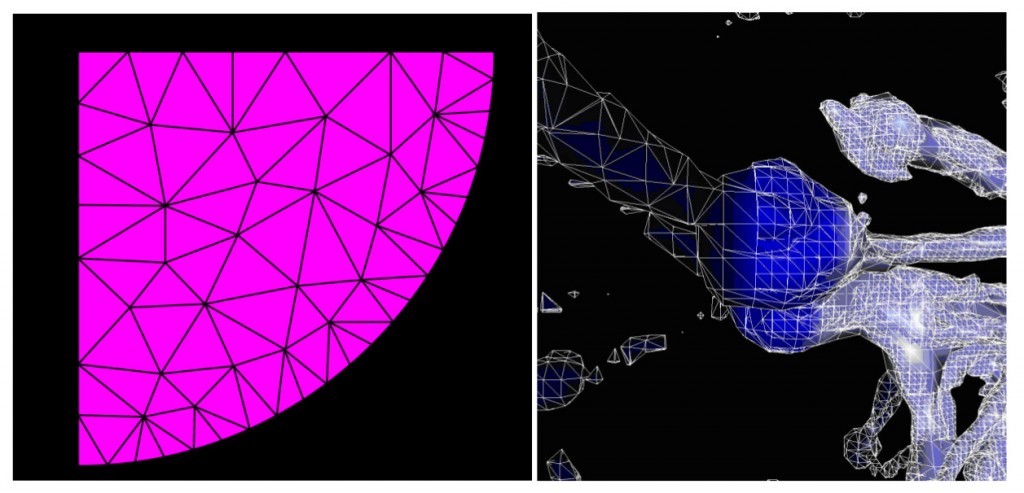
These codes have a potentially high degree of instruction parallelism, but data accesses require indirection, which increases memory operations for the indexing information and results in poor spatial locality and higher latencies for data access.
The mesh structures may be static or they may change dynamically due to changes in the physical object being simulated. They may also be hierarchical.
Forces
Precision and computational requirements: The demand for precision in the quantities being modeled pushes towards finer meshes and smaller time-steps, but the dataset size and computational requirements can grow rapidly.
Task granularity and parallelism: The problem should be broken down into tasks which may be processed in parallel, but these tasks should not be so fine-grained that the resulting overheads of invoking these tasks reduce efficiency of parallelism. Tasks which are too simple for each processing element may result in high communication and initialization overheads and not enough processor utilization which will hinder scalability, while excessively complex tasks may result in unexploited parallelism.
Simple task partitioning and load balancing: The problem should be partitioned across processing elements in a simple efficient way. However the workload associated with each subproblem might not the equal. If this is the case, we need to perform load balancing in order to ensure equal distribution of work across all processing elements.
Concurrency levels and parallel overhead: The problem contains large amount of concurrency but exploiting it effectively is difficult since the irregular nature of the data complicates data access and load balancing and increases synchronization overhead.
Flexibility of grid elements and numerical stability: Often the possible range of aspect ratios of geometric elements has to be restricted to ensure proper numerical behavior of the algorithms used.
Solution
High level solution requires the following steps:
Data Distribution
The mesh of data can be represented as a graph whose edges represent the geometric nearest-neighbor relationship between mesh points. Typically, communication patterns in mesh problems follow this nearest-neighbor relationship. That is, the value of a mesh point in the future will depend on its own value and the values of its geometric neighborhood. Partitioning such a nearest-neighbor graph to minimize the number of cross-partition edges (total edge cut) is equivalent to finding a communication-minimizing data distribution. The updates to a processor’s sub-mesh will depend on the sub-meshes of processors containing its nearest-neighbors. Since the size of sub-meshes (i.e. the number of grid-points per sub- mesh) determines the amount of work each processor is assigned, and thus the load balance of the computation, it is important for each processor’s subdomain to be of approximately equal size. Several software packages exist for solving this graph partitioning problem, possibly the most notable being Metis and Parmetis [1]. The mesh partitioning is usually performed as a preprocessing step, but adaptive algorithms may require embedded mesh partitioners that operate incrementally in response to load imbalances that are detected at runtime.
A common implementation strategy is to allocate a set of ghost regions around each processors portion of the graph, and fill this in with copies of data from neighboring node before performing each computation step. An implementation may also flatten the data structure so that the neighbors of a given entity or multiple entities may be loaded with a single memory operation.
Mesh granularity
For many problems, a statically defined mesh is sufficient to achieve the necessary numerical stability. For some highly dynamic computations, however, an Adaptive Mesh Refinement (AMR) scheme is necessary to maintain stability. The dynamic nature of an AMR mesh further substantially complicates the data distribution and load balancing problem [2]. Thus a static mesh is extremely desirable, if it is at all practical.
Numerical Solutions
Solution of differential equations over these domains are typically considered Sparse Linear Algebra problems [sparse linear algebra pattern]
Prefetching
The address resolution is typically not data-dependent for static calculations, so computations required to resolve addresses are not dependent on the computations performed on those addresses during a given iteration. A software prefetch mechanism can be used, in principle to execute the index stream because the order in which the data items are visited is static within a given iteration. However, the prefetch operations or “speculative thread” that walk ahead to resolve addresses must lead the computations by a distance equal to the product of the available memory subsystem bandwidth and latency to main memory for resolving all of the levels of indirection in order to fully saturate available bandwidth the memory interface.
Invariant
Only one or a small number of prior iterations influences the value of a future iteration.
The physics of the problem often implies conserved quantities across elements such as total flux into a volume.
Examples
Author: I could not (yet) find a good, simple, and educational one. I would like to show the following steps:
- Discretization of the geometric object
- Discretized equations
- Partitioning
The design of airfoils for airplanes requires modeling the fluid dynamics of a wing in air. In this instance, the surface of the airfoil forms is defined as a mesh of points, whose geometric properties are of import to the problem. In large, flat surfaces of the wing, the mesh can be coarse, as the dynamics on these regions will tend to be low-magnitude. At the wing-tips, however, where the surface has high curvature, a finer- granularity mesh is necessary to effectively capture the system’s properties. This leads to an irregular mesh. The problem is to solve the fluid dynamics differential equation in a series of mesh updates.
Known Uses
Solution of partial differential equations (PDE) with finite difference, element, or volume methods (FDM, FEM, FVM) and other numerical modeling of physical systems in a wide variety of engineering and science disciplines, e.g., computational fluid dynamics, structural mechanics, or electromagnetism.
Related Patterns
Structured Grids
Sparse Linear Algebra
Graph Algorithms
Authors
Erich Strohmaier (based on previous version by: Mark Murphy and N. R. Satish; and Krste Asanovic. Kathy Yelick, John Shalf, and Ras Bodik)
References
[1] Parallel static and dynamic multi-constraint graph partitioning. Kirk Schloegel, George Karypis, and Vipin Kumar. Concurrency and Computation: Practice and Experience. Volume 14, Issue 3, pages 219 – 240, 2002.
[2] Adaptive Mesh Refinement – Theory And Applications. Springer. 2005. ISBN 3540211470.