Graph Partitioning

Problem

Given a problem that can be represented as a graph with nodes and edges, how can we efficiently exploit the concurrency in this problem and map it onto parallel processing elements to guarantee efficient and load balanced execution?

Context

Many applications can be represented as a graph with a set of nodes connected by edges. The nodes and edges usually represent computation and communication. Each node and edge can have a weight that represents a particular cost of executing the computation or communication associated with it. In order to efficiently exploit parallelism in such problems, we need to decompose them among processing elements. To efficiently execute this application on a parallel platform, the computation must be load-balanced and the communication must be minimized. Graph partitioning is used to accomplish this task.

Graph Partitioning is a universally employed technique for parallelization of calculations on unstructured grids for finite element, finite difference and finite volume techniques. It is used in parallelization of matrix vector multiplication in iterative solvers such as PDE solvers using sparse matrix vector multiply. It is also used in parallelization of neural net simulations, particle calculation and VLSI circuit design.

Graph Partitioning presents a way to exploit concurrency in a problem by decomposing it into separate units to be mapped onto parallel processors. For example, after finding concurrency in a problem using the Geometric Decomposition pattern, graph partitioning can be used to divide the problem into chunks to be mapped onto parallel processors. Graph Partitioning algorithms fall into the more general category of graph algorithms, please refer to the Graph Algorithms computational pattern for more information on graph algorithms.

Forces

Generality vs specification. Representing a problem as a graph to target a specific algorithm or data structure in the problem can lead to too much specialization in the representation, making it hard to remap the problem to a different platform or data structure. However, if the problem representation is too general, it can limit the efficiency of partitioning and thus hinder the performance of the application.

Solution

In order to use graph partitioning to exploit concurrency in a given application we must:

1. Find a graph representation model for the problem:

a. Assign nodes and edges

b. Assign weights

c. Pick a graph structure

2. Choose a graph partitioning algorithm

The formal definition of a graph partitioning problem is as follows:

 

GraphG=(N,E,W_N,W_E)

• N = nodes (or vertices),
• W_N = node weights
• E = edges
• W_E = edge weights

Example: N = {tasks}, W_N = {task costs}, edge (j,k) in E means task j sends W_E(j,k) words to task k
Graph partitioning is the task to choose a partition N = N₁  ∪ N₂ ∪ … ∪ N_p such that

1. The sum of the node weights in each N_j is close to equal
2. The sum of all edge weights of edges connecting all different pairs N_j and N_k is minimized

1. Find a representation model

First we need to find a good graph representation model for a given problem. We need to assign nodes and edges of the graph.

Assigning nodes. If the problem’s computation can be decomposed into tasks, each node in the graph can be assigned a task. In some cases, if the problem graph is too large to fit in memory, the graph can be coarsened with each node representing a group of tasks, this can also help accelerate the computation.

Assigning edges: Edges represent connections between the tasks (nodes) in the problem. They can be either data dependencies or task dependencies.

1. Edges as data dependencies. This is the more intuitive way to think about graph representations. Each task needs some data to perform its computation with data dependencies among the tasks. During the program’s execution, the tasks need to communicate to get the data they need in order to perform their computations. On a distributed memory platform this is implemented using message sends and receives. On a shared memory this is implemented with tasks accessing the data in memory and using locks to guarantee atomicity and order control.
2. Edges as task dependencies. The tasks have to execute in a particular order, where one task has to wait for another to finish before continuing its own computation. This type of problem is represented via a directed graph, where there are directed edges coming out of nodes representing the order in which tasks must be executed.

Assigning weights. Each task (node) and each dependency (edge) can have a weight associated with it representing the computational or communication cost of that entity. For example, a task might take a certain number of compute cycles to execute or a dependency might take a certain number of bytes to be sent across the network to be fulfilled. Depending on the problem structure, assigning weights might help to get a better partition.

Picking graph structure. After assigning nodes and edges of the graph to tasks and dependencies of our problem, we need to pick a graph structure that best represents the problem. There are several various types of graph structures: bipartite graph, directed graph, undirected graph, and hypergraph.

1. Bipartite graph. If the problem needs to be decomposed into only two sets, bipartite graph is the best one to choose. The bipartite graph is defined as a graph whose nodes belong to two disjoint sets with no edges between nodes in the same set. Bipartite graphs are usually used for matching problems. For example, if we want to find a maximum matching from a set of features to a character in the optical character recognition problem.
2. Directed graph. If the problem is composed of tasks that are time dependent, it is easiest to represent the problem as a directed graph. Each node of the graph represents a task and each edge is *directed*, i.e. it represents a time dependency between a pair of tasks showing that one task cannot be executed before another one completes.
3. Undirected graph. A graph that contains edges that are undirected, representing a relationship between nodes that is the same in both directions, i.e. from node x to y the dependency is the same as from node y to x.
4. Hypergraph. This graph is more general. It’s nodes are computational tasks and its edges are communication dependencies, however each edge connects a set of nodes, instead of just two. The hypergraph model is well suited to parallel computing, where vertices correspond to data objects and hyperedges represent the communication requirements. The basic partitioning problem is to partition the vertices into k approximately equal sets such that the number of cut hyperedges is minimized. Hypergraphs provide more accurate partitions, since the communication can be modeled exactly as the communication volume.

2. Find a decomposition algorithm

After selecting a graph representation of the problem, we need to pick a partitioning algorithm. Graph partitioning is an NP-complete problem. As the problem size increases, the time to find the optimal solution increases exponentially. Thus, we need to use good heuristics to find a partitioning that is close to optimal. Graph partitioning can be done by recursively bisecting a graph or directly partitioning it into k sets.

There are two ways to partition a graph, by taking out edges, and by taking out vertices. Graph partitioning algorithms use either edge or vertex separators in their execution, depending on the particular algorithm. We define the two sets as follows:

An edge-separator, Es (subset of E) separates G if removing Es from E leaves two approximately equal-sized disconnected components of N: N₁  ∪ N₂.
A vertex-separator, Ns (subset of N) separates G if removing Ns and all incident edges leaves k approximately equal-sized disconnected components of N: N₁  ∪ N₂.

Partitioning Algorithms

Among various techniques, we will discuss Breadth First Search (BFS), Kerninghan-Lin (KL) algorithm, Fiduccia-Mattheyses (FM) algorithm and Spectral Bisection and k-way partitioning method. KL, FM and Spectral Bisection perform graph bisection. To partition a graph into k partitions, we recursively call the graph bisection algorithm until we have k partitions. K-way partition algorithm directly partitions the graph into k partitions.

1. BFS

The well-known BFS (Breadth-First-Search) algorithm can also be used for graph partitioning. BFS algorithm traverses the graph level by level and marks each vertex with the level in which it was visited. After completion of the traversal, the set of vertices of the graph is portioned into two parts V₁ and V₂ by putting all vertices with level less than or equal to a pre-determined threshold L in the set V₁ and putting the remaining vertices (with level greater than L) in the set V₂. L is so chosen that |V₁| is close to |V₂|.

2. Kernighan-Lin Algorithm

Synopsis: The Kernighan-Lin algorithm (KL algorithm hereafter) is one of the oldest heuristic graph partitioning algorithms proposed in 1970 [6]. In the simplest possible setting, KL algorithm takes an edge-weighted graph G = (V, E, edge-weight function c) with 2n vertices and an initial bi-partition (V₁, V₂) of the vertex set V where |V₁| = |V₂| = n and produces a new partition (V₁’, V₂’) such that |V₁’| = |V₂’| = n and the total cost of the new partition is lower than (or equal to) the cost of the original partition. Note that KL algorithm is a balanced partitioning algorithm i.e. the two parts produced by KL algorithm have the same (or almost same, in a more general setting) number of vertices. It iteratively swaps pairs of vertices until it reaches a locally optimal partition and runs in time O(N^3) where N is the number of vertices in G (for example, N = 2n when we assume that we started with a graph with 2n vertices). Fiduccia-Mattheyeses algorithm improved the approach of KL algorithm to run in O(E) time and to work on hypergraphs as well. Since KL algorithm forms the foundation of a subsequent family of the state-of-the-art graph partitioning algorithms, we will describe its working principle in detail in the following section.

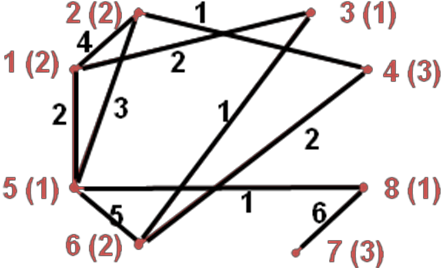
Detailed Description of KL algorithm: Let G = (V, E, c) be an undirected graph where V is the set of vertices, E is the set of edges and c is the edge-weight function such that c(u,v) denotes the weight of the edge between vertex u and vertex v. If there is no edge between u and v, we will assume that c(u,v) = 0. Let (V₁, V₂) be an initial partition. The cost of a partition (V₁, V₂), denoted as cost(V₁, V₂), is defined as the sum of weights of all the edges (u,v) crossing the partition i.e. where u and v belong to two different partitions. Let us take an illustrative example to explain the above concept. This example is taken from [7] and will serve as our running example in this disposition.

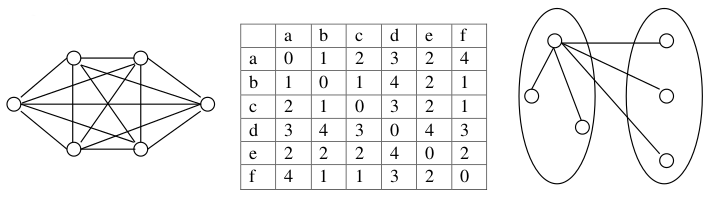Figure above shows a complete graph with 6 vertices and the corresponding edge weight matrix is shown in the Figure. This represents an initial partition (V₁, V₂) where V₁ = {a, b, c} and V₂ = {d, e, f}. Therefore, The cost of this partition, cost( {a, b, c}, {d, e, f} ) = (3+2+4)+(4+2+1)+(3+2+1) = 22.

For any vertex a ∈  V₁, define external cost of a as E_a =  ∑ c(a,v) where v  ∈ V₂ and internal cost of a ∈ V₁ as I_a = ∑ c(a,v) where v   V₁. Also define D_a = E_a – I_a. Similarly, define E_b, I_b and D_b for any vertex b V₂. Note that D_a denotes the amount by which the cost of the initial partition (V₁, V₂) will be reduced if we move vertex a from its present partition to the complementary partition. Now, let a V₁ and b V₂. If we swap a and b, the net reduction in the cost of the partition is g_ab = D_a + D_b – 2c(a, b). In the first iteration of KL algorithm, D-values of all vertices and g-values of all candidate pairs for swapping are calculated and the pair of vertices (a, b) is found out where a ∈ V₁ and b ∈ V₂ and gab  is maximum among all other candidate pairs. Then a and b are swapped and locked for all subsequent iterations. By locking we mean that once we swap a and b, neither a nor b will be considered for swapping in any of the following iterations. This first step of KL algorithm on the initial partition of Figure [refer] will produce the following E_x, I_x, D_x and g_xy:

I_a = 1 + 2 = 3; E_a = 3 + 2 + 4 = 9; D_a = E_a – I_a = 9 – 3 = 6
I_b = 1 + 1 = 2; E_b = 4 + 2 + 1 = 7; D_b = E_b – I_b = 7 – 2 = 5
I_c = 2 + 1 = 3; E_c = 3 + 2 + 1 = 6; D_c = E_c – I_c = 6 – 3 = 3
I_d = 4 + 3 = 7; E_d = 3 + 4 + 3 = 10; D_d = E_d – I_d = 10 – 7 = 3
I_e = 4 + 2 = 6; E_e = 2 + 2 + 2 = 6; D_e = D_e – I_e = 6 – 6 = 0
I_f = 3 + 2 = 5; E_f = 4 + 1 + 1 = 6; D_f = D_e – I_e = 6 – 5 = 1

Remember that g_xy = D_x + D_y – 2c(x, y) and it has to be computed for all candidate pairs for swapping. Therefore, g_ad = 6 + 3 – 2 * 3 = 3. Similarly, g_ae = 2, g_af = -1, g_bd = 0, g_be = 1, g_bf =4, g_cd =0, g_ce = -1and g_cf =2. Since g_ab is the maximum among all other candidate pairs, we select b and f for swapping in this iteration; we swap them and lock them. g_bf will be referred to as the gain of iteration 1 and denoted as g₁. Swapping and locking of b and f leaves (a, d), (a, e), (c, d) and (c, e) as the possible candidate pairs for the next swapping. But note that D-values of all the unlocked vertices must be updated due to the swapping of b and f. The update rule is as follows:

If  a ∈  V1 and b ∈  V2 and they are swapped, then

for all x ∈ V1\{a}, Dx’ = Dx + 2c(x, a) – 2c(x, b)

for all y ∈ V2\{b}, Dy’ = Dy + 2c(y, b) – 2c(y, a)

Applying the above update rule to our running example, we update the following D -values D_a’ = 6 + 2*1 – 2*4 = 0; similarly D_c’ = 3, D_d’ = 1, D_e’ = 0

Now we iterate the same step as above to calculate the g-values of all possible candidate pairs for swapping and choose the pair with maximum g-value. This gives the following values: g_ad  = -5, g_ae  = -4, g_cd  = -2, g_ce  = -1. Now, g_ce  is the maximum and, therefore, we select the pair (c. e) for swapping; we swap them and lock them leaving only (a, d) as the candidate pair for next swapping. Again, g_ce is referred to as the gain of second iteration and denoted as g₂.

We again update the D-values of the unlocked vertices. In this case D_a’’ = 0 and D_d” = 3 and g_ad = -3. We swap a and d and lock them. This completes the sequence of iterations of KL algorithm since there is no more pairs to be swapped. g_ad is again referred to as the gain of third iteration and denoted as g₃.

In this way, we run k iterations of KL algorithm on an initial bi-partition of a given graph with 2k vertices and we get a sequence g₁, g₂, …, g_k of gains. Now we find out an integer k’ where 1 <= k’ <= k such that g₁ + g₂ + … + g_k is the maximum for all possible k’. KL algorithm then modifies the initial partition by swapping all the candidate pairs upto the k`-th iteration. This produces a partition with locally minimum cost. In our example, g₁ has the maximum value among g₁, g₁ + g₂, and g₁ + g₂ + g₃. Hence KL algorithm modifies the initial partition by swapping b and f only.

Pseudocode of KL algorithm

Compute T = cost(A,B) for initial A, 
    B Repeat
        Compute costs D(n) for all n in N
        Unmark all nodes in N
        While there are unmarked nodes
            Find an unmarked pair (a,b) maximizing gain(a,b)
            Mark a and b (but do not swap them) Update D(n) for all unmarked n,
              as though a and b had been swapped
        Endwhile

        Pick m maximizing Gain = Sk=1 to m gain(k) 
        If Gain > 0 then … it is worth 
        swapping
            Update newA = A - { a1,…,am } U { b1,…,bm }
            Update newB = B - { b1,…,bm } U { a1,…,am 
                } Update T = T - Gain
        endif 
    Until Gain <= 0

3. Fiduccia-Mattheyses Partitioning Algorithm

Fiduccia-Mattheyeses algorithm (FM algorithm hereafter) is another heuristic partitioning algorithm which generalizes the concept of swapping of nodes introduced in KL algorithm. To contrast FM algorithm with KL algorithm, FM algorithm is designed to work on hypergraphs and instead of swapping a pair of nodes as was happening in KL algorithm, FM algorithm swaps a single node in each iteration. The basic essence of FM algorithm is the same as KL algorithm – we define gains for each vertex of the (hyper)graph, select one node according to some criterion, remove it from its present partition and put it to the other partition, lock that vertex, update gains of all other unlocked vertices and iterate these steps until we reach a local optimum configuration. The tool hMETIS implements an augmented version of FM algorithm (please refer to Existing tools for Graph Partitioning section).

4. Spectral Bisection

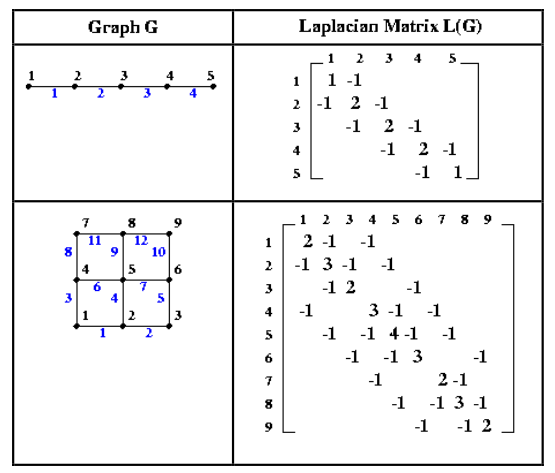
The theory of spectral bisection was developed by Fiedler in 1970 and it was popularized by Pother, Simon and Liou in 1990. It is based on eigen-vector computation of the ‘Laplacian matrix’ of the graph under consideration. For a graph G, we define its Laplacian matrix L(G) in the following way:

Definition: The Laplacian matrix L(G) of a graph G = (V, E) is a |V| x |V| symmetric matrix with one row and one column for each vertex and the entries of the matrix is defined as follows:

a. L(G)(i, i) = degree of node i (number of incident edges)

b. L(G)(i, j) = -1 if i ≠ j and there is an edge (i, j)

c. L(G)(i, j) = 0, otherwise

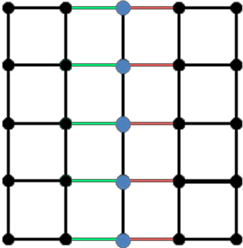
Below we present two very simple mesh graphs and their Laplacian matrices for the purpose of illustration. The black numbers (on the vertices) represent the vertex identifies and the blue numbers (on the edges) represent the edge identifiers. For our current discussion, we may ignore the edge identifiers.

Spectral Bisection Algorithm:

• Construct the Laplacian matrix L(G) for the input graph G = (V, E)
• compute the eigenvector v₂ corresponding to the second eigenvalue λ₂ of the Laplacian matrix L(G)
• For each vertex i ∈ V,
  • if v₂[i] < 0 put vertex I in partition V^(-)
  • else put vertex I in partition V⁽⁺⁾

For motivation and justification of the above algorithm, please see [1]. The key computational steps of this algorithm is determination of λ₂ and v₂ of L(G). In practice, it is performed using Lanczos algorithm [1].

5.  k -way partitioning

K-way partitioning method can be used to directly partition a graph into k sets.

The k-way The k-way hypergraph partitioning problem is defined as follows: Given a hypergraph G=(V, E) (where V is the set or vertices and E is the set of hyperedges) and an overall load imbalance tolerance c such that c>=1.0, the goal is to partition the set V into k disjoint subsets, V₁,V₂, . . . ,V_k such that the number of vertices in each set V_i is bounded by |V|/(ck)<=|V_i|<=c|V|/k, and a function defined over the hyperedges is optimized [9].

The requirement that the size of each partition is bounded is referred to as the partitioning constraint, and the requirement that a particular function is optimized is referred to as the partitioning objective. Some examples of objective functions include minimizing the hyperedge-cut (the total number of hyperedges that span the partition) or to minimize the sum of external degrees (the number of partitions all the hyperedges that cross the partitioning boundary span).

Here we describe a greedy algorithm to do k-way graph partitioning, shown in [9]. It produces high quality partitioning in small amount of time.

The greedy algorithm consists of a number of iterations. In each iteration it checks all the vertices to see if they can be moved to any of the k partitions so that the partitioning objective function is optimized. The algorithm works as follows:

Consider a hypergraph G_i=(v_i, E_i), and its partitioning vector P_i. The vertices are visited in a random order. Let v be such a vertex, let P_i[v]=a be the partition that v belongs to. If v is a node internal to partition a then v is not moved. If v is at the boundary of the partition, then v can potentially be moved to one of the partitions N(v) that vertices adjacent to v belong to. Let N’(v) be the subset of N(v) that contains all partitions b such that movement of vertex v to
partition b does not violate the balancing constraint. Now the partition b ϵ N’(v) that leads to the greatest positive reduction (gain) in the objective function is selected and v is moved to that partition. The iterations repeat till the algorithm converges to an optimal k-way partition.

It is beneficial in some cases to do direct k-way partitioning instead of recursive bisection as it allows for direct optimization of global objectives such as the sum of external edges and scaled cost . It is also capable of enforcing tighter balancing constraints while retaining the ability to sufficiently explore the solution space of the partitioning problem [9].

Existing tools for Graph Partitioning

There are several graph partitioning tools available. We discuss several of them here and give references of where to find more information.

ParMETIS

ParMETIS [2] is an MPI-based parallel library that includes algorithms for partitioning unstructured meshes and graphs and for computing fill-reducing orderings of sparse matrices. It is designed especially for large numerical simulation codes. The algorithms it implements are based on k-way multilevel graph-partitioning and adaptive repartitioning. It performs graph partitioning quickly, taking advantage of geometry information. It also computes graph repartitioning and refinement and optimizes both the number of vertices that are moved and the edge-cut of the resulting problem.

hMETIS

hMETIS [3] is a set of programs developed for partitioning hypergraphs. This is useful in the VLSI circuit design using multilevel hypergraph partitioning schemes. The algorithms in hMETIS are very fast and are of high quality.

Zoltan

Zoltan [4] is a tool developed by the Sandia National Laboratories. Zoltan is a collection of data management software for parallel, unstructured, adaptive and dynamic applications. Among several things, it simplifies load balancing and data movement in dynamic applications. It includes a suite of parallel partitioning algorithms, in particular it performs graph partitioning. Zoltan provides three packages capable of partitioning a graph: PHG (it’s own default), and ParMETIS [2] and Jostle [5] as external packages that it supports. PHG is Zoltan’s native hypergraph partitioner. It allows for a flexible graph model where edges and nodes both can be assigned a weight.

Jostle

Jostle [5] is a software package that is designed to partition unstructured meshes for use on distributed memory parallel computers. It uses an undirected graph model to represent the mesh and then uses graph partition to partition the mesh across computing nodes.

Invariant

The structure of the dependencies between tasks is preserved independent of the partition.

Examples

1. Sparse matrix-vector multiply.

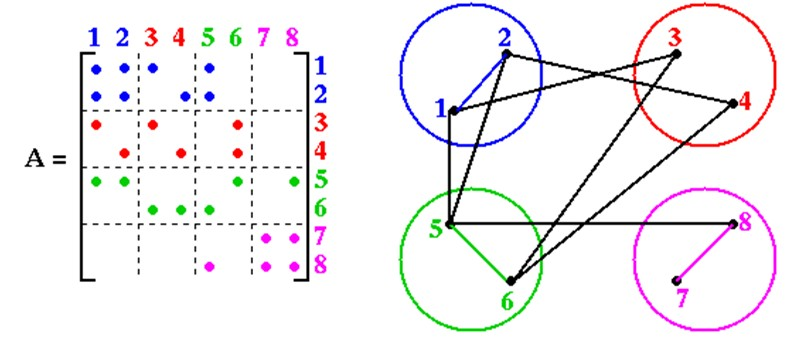
The problem is as follows, given a sparse n x n matrix A with some non-zero elements and a vector x, we want to compute y = y+ A*x. A sample illustration of the matrix is as follows:

Figure 1. Sparse matrix representation using a graph.

In order to efficiently exploit the concurrency in this problem, we must efficiently map the tasks onto processing elements and minimize communication. Representing this problem as a graph and using graph partitioning helps accomplish this task.

1. Finding a representation model

1. Assigning nodes and edges

To represent this matrix as a graph, we assign each entry index to a node, thus N = {1…n} and each edge connects two nodes if there is a non-zero entry between the two entries. For example, in the above matrix, there is a non-zero entry in A[2, 1] which corresponds to the edge between the nodes 1 and 2 in the graph.

2. Picking graph structure

If the matrix is symmetric, the graph is undirected graph, since each edge corresponds to a non – zero entry in the matrix and A[i,j] = A[j, i]. If the matrix is non-symmetric, this graph would have directed edges from node i to node j corresponding to a non-zero entry of A[i,j].

This is a planar graph, since we can draw it on a piece of paper without any edges crossing each other. The graph corresponding to a sample sparse matrix is shown in Figure 1.

2. Finding a decomposition algorithm

Since the matrix is not symmetric, we cannot use Spectral Bisection method, and we cannot use the FM algorithm since the graph is not a hypergraph. Thus, to partition this graph we can use the k- way partitioning algorithm or recursive bipartition using Kernighan-Lin algorithm. Recursive bipartition using KL will yield better results, however, thus, it is the preferred method.

References

1. James Demmel. CS267 lecture 13 – Graph Partitioning. http://www.cs.berkeley.edu/~demmel/cs267_Spr09/Lectures/lecture13_partition_jwd09.ppt

2. ParMETIS – Parlalel Graph Partitioning and Fill-reducing Matrix Ordering. http://glaros.dtc.umn.edu/gkhome/metis/parmetis/overview

3. hMETIS – Hypergraph & Circuit Partitioning. http://glaros.dtc.umn.edu/gkhome/metis/hmetis/overview

4. Zoltan: Parallel Partitioning, Load Balancing and Data-Management. http://www.cs.sandia.gov/Zoltan/

5. Jostle – Graph Partitioning Software. http://www.cs.sunysb.edu/~algorith/implement/jostle/implement.shtml

6. Kernighan, B.W. and Lin, S. An efficient heuristic procedure for partitioning graphs. The Bell System Technical Journal, 49(2):291-307. 1970

7. Prof Yao-Wen Chang’s course page: http://cc.ee.ntu.edu.tw/~ywchang/Courses/PD/pd.html

8. C. M. Fiduccia and R. M. Mattheyses , A Linear-Time Heuristic for Improving Network Partitions, DAC 1982

9. George Karypis and Vipin Kumar. Multilevel k-way Hypergraph Partitioning. VLSI Design, Vol. 11, No. 3, pp. 285-300, 2000.

Authors

Katya Gonina, Sayak Ray, Bor-Yiing Su