A Design Pattern Language for Engineering (Parallel) Software

Kurt Keutzer (EECS UC Berkeley) and Tim Mattson (Intel)

The key to writing high quality parallel software is to develop a robust software design. This applies to the overall architecture of the program, but also to the lower layers in the software system where the concurrency and how it is expressed in the final program is defined. Technology to more systematically describe such designs and reuse them between software projects is the fundamental problem facing software for terascale processors. This is far more important than programming models and their supporting environments, since with a good design in hand, most any programming system can be used to actually generate the program’s source code.

In this paper, we will develop our thesis about the central role played by the architecture/design for software. We will then show how design patterns provide a technology to define the reusable design elements in software engineering. This leads us to the ongoing project centered at UC Berkeley’s Par Lab to pull the essential set of design patterns for parallel software design into a Design Pattern Language. After describing out pattern language, we’ll present a case study from the field of machine learning as a concrete example of how patterns are used in practice.

The software engineering crisis

The trend has been well established [Asanovic09]: parallel processors will dominate most if not every niche of computing. Ideally, this transition would be driven by the needs of software. Scalable software would demand scalable hardware and that would drive  CPU’s to add cores. But this is not the case. The motivation for parallelism comes from the inability to deliver steadily increasing frequency gains without pushing power dissipation to unsustainable levels. Thus, we have a dangerous mismatch; the semiconductor industry is banking its future on parallel microprocessors, while the software industry is still searching for an effective solution to the parallel programming problem.

The parallel programming problem is not new. It has been an active area of research for the last three decades. And we can learn a great deal from what has not worked in the past.

• Automatic parallelism: Compilers can speculate, prefetch data and reorder instructions to balance the load among the components of a system. But they can not look at a serial algorithm and create a different algorithm better suited for parallel execution.

• New languages: Hundreds of new parallel languages and programming environments have been created over the last few decades. Many of them are excellent and provide high level abstractions that simplify the expression of parallel algorithms. But these languages have not dramatically grown the pool of parallel programmers. The fact is, in the one community with a long tradition of parallel computing (high performance computing) the old standards of MPI and OpenMP continue to dominate. There is no reason to believe new languages will be any more successful as we move to more general purpose programmers; i.e. it is not the quality of our programming models that is inhibiting the adoption of parallel programming.

The central cause of the parallel programming problem is fundamental to the enterprise  of programming itself. In other words, we believe that our challenges in programming parallel processors point to deeper challenges in programming software in general. We believe the only way to solve the programming problem in general is to first understand how to architect software. Thus we feel that the way to solve the parallel programming problem is to first understand how to architect parallel software. Given a good software design grounded on solid architectural principles, a software engineer can produce high quality and scalable software. Starting with an ill-suited sense of the architecture for a software system, however, almost always leads to failure. Therefore it follows that the first step in addressing the parallel programming problem is to focus on software architecture. From that vantage point, we have a hope of choosing the right programming models and building the right software frameworks that will allow the general population of programmers to produce parallel software.

In this paper, we describe our work on software architecture. We use the device of a pattern language to write our ideas down and put them into a systematic form that can be used by others. After we present our pattern language [OPL09], we present a case study to show how these patterns can be used to understand software architecture.

Software architecture and design patterns

Productive, efficient software follows from good software architecture. Hence, we need to develop a theory of how software is architected, and in order to do this we need a way to write down architectural ideas in a form that groups of programmers can study, debate, and come to consensus on. This systematic process has at its core the peer review  process that has been instrumental in advancing scientific and engineering disciplines.

The prerequisite to this process is a systematic way to write down the design elements from which anarchitecture is defined. Fortunately, the software community has already reached consensus on how write these elements down: design patterns [Gamma94].

Design patterns give names to solutions to recurring problems that experts in a problem- domain gradually learn and “take for granted.” It is the possession of this tool-bag of solutions, and the ability to apply them with facility, that precisely defines what it means to be an expert in a domain.

For example, consider the Dense-linear- algebra pattern. Experts in fields that make heavy use of linear algebra have worked out a family of solutions to these problems. These solutions have a common set of design elements that can be captured in a Dense- Linear-Algebra design pattern. We summarize the pattern in the sidebar, but it is important to know that in the full text to the pattern [OPL09] there would be sample code, examples, references, invariants and other information needed to guide a software developer interested in dense linear algebra problems.

The dense linear algebra pattern is just one of the many patterns a software architect might use when designing an algorithm. A full design includes high-level patterns that describe how an application is organized,  midlevel patterns about specific classes of computations, and low level patterns  describing specific execution strategies. We can take this full range of patterns and organize them into a single integrated pattern language – a web of interlocking of patterns that guide a designer from the beginning of a design problem to its successful realization ([Alexander72][Mattson04]).

To represent the domain of software engineering in terms of a single pattern language is a daunting undertaking. Fortunately, based on our studies of successful application software, we believe software architectures can be built up from a manageable number of design patterns. These patterns define the building blocks of all software engineering and are fundamental to the practice of architecting parallel software.  Hence, an effort to propose, argue about, and finally agree on what this set of patterns are is the seminal intellectual challenge of our field

Our Pattern Language

Software architecture defines the components that make up a software system, the roles played by those components, and how they interact. Good software architecture makes design choices explicit and the critical issues addressed by a solution clear. A software architecture is hierarchical rather than monolithic. It lets the designer localize problems and define design elements that can be reused from one problem to another.

The goal of OPL is to encompass the complete architecture of an application; from the structural patterns (also known as architectural styles) that define the overall organization of an application [Garlan94] [Shaw95], to the basic computational patterns (also known as computational motifs) for each stage of the problem [Asanovic06][Asanovic09], to the low level details of the parallel algorithm [Mattson04].  With such a broad scope, organizing our design patterns into a coherent pattern language was extremely challenging.

Our approach is to use a layered hierarchy of patterns. Each level in the hierarchy addresses a portion of the design problem. While a designer may in some cases work through the layers of our hierarchy “in order”, it is important to appreciate that many design problems do not lend themselves to a top-down or bottom-up analysis. In many cases, the pathway through our patterns will be bounce around between layers with the designer working at whichever layer is most productive at a given time (so called opportunistic refinement). In other words, while we use a fixed layered approach to organize our patterns into OPL, we expect designers will work though the pattern language in many different ways. This flexibility is an essential feature of design pattern languages.

Figure 1 The structure of OPL and the five categories of design patterns.

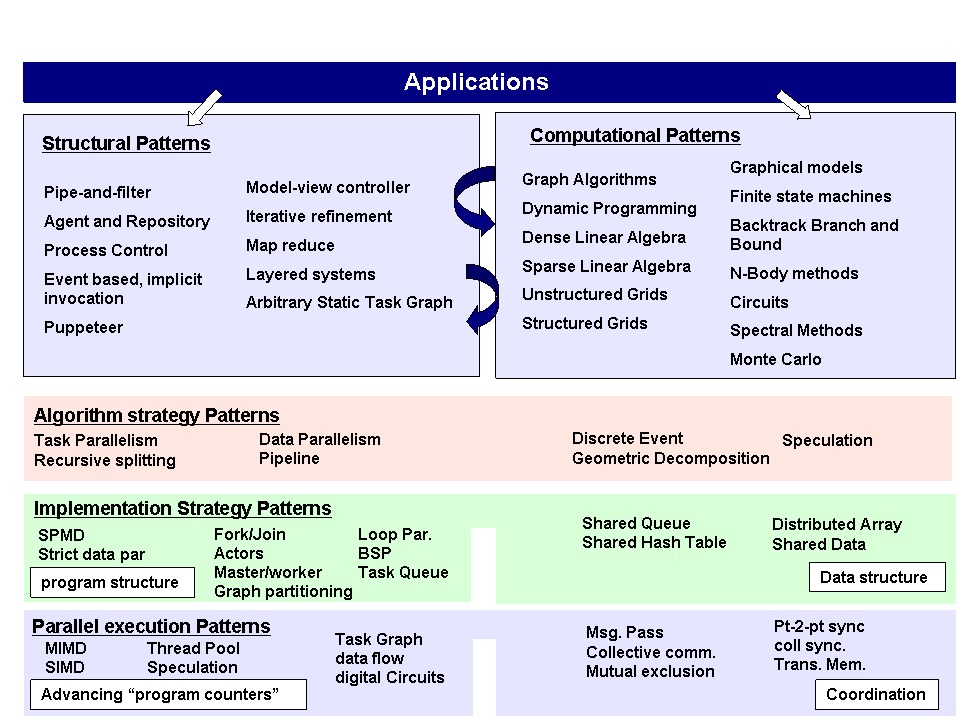
As shown in Figure 1, we organize OPL into five major categories of patterns. Categories one and two sit at the same level of the hierarchy, and cooperate to create one layer of the software architecture.

1. Structural patterns: Describe the overall organization of the application and the way the computational elements that make up the application interact. These patterns are closely related to the architectural styles discussed in [Garlan94]. Informally, these patterns correspond to the “boxes and arrows” and architect draws to describe the overall organization of an application. An example of a structural pattern is pipe-and- filter described in the sidebar.
2. Computational patterns: These patterns describe the classes of computations that make up the application. They are essentially the thirteen motifs made famous in [Asanovic06] but described more precisely as patterns rather than simply computational families. These patterns can be viewed as defining the “computations occurring in the boxes” defined by the structural patterns. A good example is the dense-linear-algebra pattern described in an earlier sidebar. Note that some of these patterns (such as graph algorithms or N-body) define complicated design problems in their own right and serve as entry points into smaller design pattern languages focused on a specific class of computations. This is yet another example of the hierarchical nature of the software design problem.

In OPL, the top two categories, the structural and computational patterns, are placed side by side with connecting arrows. This shows the tight coupling between these patterns and the iterative nature of how a designer works with them. In other words, a designer thinks about his or her problem, chooses a structure pattern, then considers the computational patterns required to solve the problem. The selection of computational patterns may suggest a different overall structure for the architecture and force a reconsideration of the appropriate structural patterns. This process, moving between structural and computational patterns, continues until the designer settles on a high level design for the problem.

The structural and computational patterns are used in both serial and parallel programs. Ideally, the designer working at this level, even for a parallel program, will not need to focus on parallel computing issues. For the remaining layers of the pattern language, parallel programming is a primary concern.

Parallel programming is the art of using concurrency in a problem to make the problem run to completion in less time. We divide the parallel design process into the following three layers.

1. Concurrent Algorithm strategies: These patterns define high-level strategies to exploit concurrency in a computation for execution on a  parallel computer. They address the different ways concurrency is naturally expressed within a problem providing well known techniques to exploit that concurrency. A good example of an algorithm strategy pattern is the Data Parallelism pattern.
2. Implementation strategies: These are the structures that are realized in source code to support (a) how the program itself is organized and (b) common data structures specific to parallel programming. The loop parallel pattern is a well known example of an implementation strategy pattern.
3. Parallel execution patterns: These are the approaches used to support the execution of a parallel algorithm. This includes (a) strategies that advance a program counter and (b)   basic building blocks to support the coordination of concurrent tasks. The SIMD pattern is a good example of a parallel execution pattern.

There is a large intellectual history leading up to OPL. The structural patterns of Category 1 are largely taken from the work of Garlan and Shaw on architectural styles [Garlan94] [Shaw95]. That these architectural styles could also be viewed as design patterns was quickly recognized by Buschmann [Buschmann96]. To Garlan and Shaw’s architectural styles we added two structural patterns that have their roots in parallel computing: Map Reduce, influenced by [Dean04] and Iterative Refinement, influenced by Valiant’s bulk-synchronous pattern [Valiant90]. The computation patterns of Category 2 were first presented as “dwarfs” in [Asanovic06] and their role as computational patterns was only identified later [Asanovic09]. The identification of these computational patterns in turn owes a debt to Phil Colella’s unpublished work on the “Seven Dwarfs of Parallel Computing.” The lower three Categories within OPL build off earlier and more traditional patterns for parallel algorithms [Mattson04]. Mattson’s work was somewhat inspired by Gamma’s success in using design patterns for object-oriented programming [Gamma94]. Of course all work on design patterns has its roots in Alexander’s ground-breaking work identifying design patterns in civil architecture [Alexander72].

Case Study: Content Based Image retrieval

Experience has shown that an easy way to understand patterns and how they are used is to follow an example. In this new section we will describe a problem and its parallelization using patterns from OPL. In doing so we will describe a subset of the patterns and give some indication of the way we make transitions between layers in the pattern language.

In particular, to understand how OPL can help software architecture, we use a content- based image retrieval (CBIR) application as an example. From this example we will show how structural and computational patterns can be used to describe the CBIR application and how the lower layer patterns can be used to parallelize an exemplar component of the CBIR application.

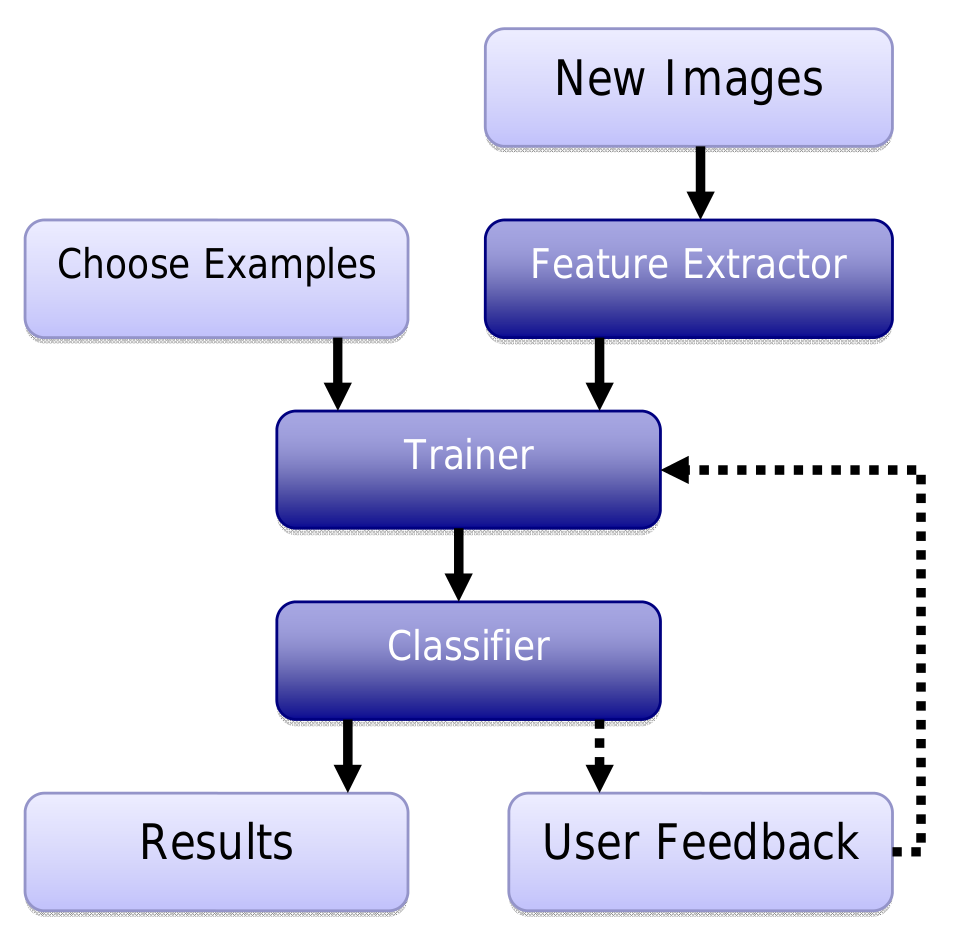
In Figure 2 we see the major elements of our CBIR application as well as the data flow. The key elements of the application are the feature extractor, the trainer, and the classifier components. Given a set of new images the feature extractor will collect features of the images. Given the features of the new images, chosen examples, and some classified new images from user feedback, the trainer will train the parameters necessary for the classifier. Given the parameters from the trainer, the classifier will classify the new images based on their features. The user can classify some of the resulting images and give feedback to the trainer repeatedly in order to increase the accuracy of the classifier. This top level organization of CBIR is best represented by the pipe-and-filter structural pattern. The feature-extractor, trainer, and classifier are filters or computational elements which are connected by pipes (data communication channels). Data flows through the succession of filters which do not share state and only take input from their input pipe(s). The filters perform the appropriate computation on that data and pass the output to the next filter(s) via its output pipe. The choice of pipe-and-filter pattern to describe the top level structure of CBIR is not unusual. Many applications are naturally described by pipe- and-filter at the top level.

In our approach we architect software using patterns in a hierarchical fashion. Since each of the filters of CBIR are complex computations they can be further decomposed. In the following discussion we consider the classifier filter. There are many approaches to

Figure 2: The CBIR application framework.

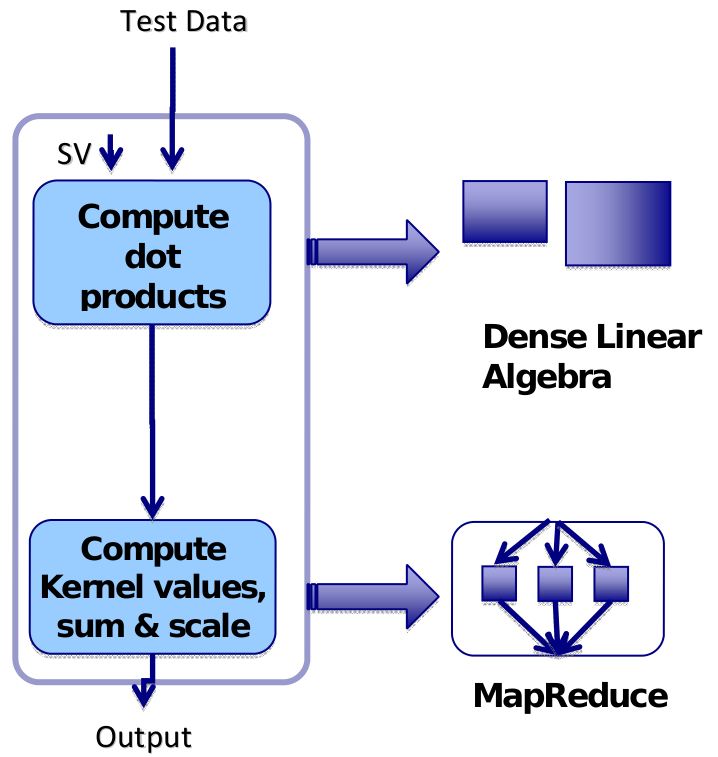
classification but in our CBIR application we use a support-vector machine (SVM) classifier. SVM is widely used in many classification tasks such as image recognition, bioinformatics, and text processing. The structure and computations in the SVM classifier are described in Figure 3. The basic structure of the classifier filter is itself a simple pipe- and-filter structure with two filters: The first filter takes the test data and the support vectors needed to calculate the dot products between the test data and each support vector. This dot product computation is naturally performed using the dense linear algebra computational pattern. The second filter takes the resulting dot products and the following steps are to compute the kernel values, sum up all the kernel values, and scale the final results if necessary. The structural pattern associated with these computations is MapReduce (see the MapReduce sidebar).

In a similar way the feature-extractor and trainer filters of the CBIR application can be decomposed. With that elaboration we would consider the “high-level” architecture of the CBIR application complete. In general, to construct a high-level architecture of an application we hierarchically decompose the application using  the structural and computational patterns of OPL.

After identifying the structural patterns and the computational patterns in the SVM classifier, we need to find appropriate strategies to parallelize the computation. In the MapReduce pattern the same computation is mapped to different non-overlapping partitions of the state set. The results of these computations are then gathered, or reduced. If we are interested in arriving at a parallel implementation of this computation then we define the MapReduce structure in terms of a Concurrent Algorithmic Strategy. The natural choices for Algorithmic Strategies are the data parallelism and geometric decomposition patterns. Using data parallelism we can compute the kernel value of each dot product in parallel(see the data parallelism side bar).Alternatively, using geometric decomposition(see the geometric decomposition sidebar) we can divide the dot products into regular chunks of data, apply the dot products locally on each chunk,and then apply a global reduce to compute the summation over all chunks for the final results. We are interested in designs that can utilize large numbers of cores. Since the solution based on the Data parallelism pattern exposes more concurrent tasks (due to the large numbers of dot products) compared to the more coarse grained to geometric decomposition solution, we choose the data parallelism pattern for implementing the map reduce computation.

Figure 3: Architecture of the SVM classifier filter

To implement the data parallelism strategy from the MapReduce pseudo-code, we need to find the best Implementation Strategy Pattern. Looking at the patterns in OPL, both strict data parallel and loop parallel are applicable.

Whether we choose either strict data parallel or loop parallel in the implementation layer, we can use the SIMD pattern for realizing the execution. For example, we can apply  SIMD on line 2 in Figure 4 for calculating the kernel value of each dot product in parallel.

function ComputeMapReduce( DataArray, Result) {

1 for i ← 1 to n {
2 LocalValue[i] ← ComputeKernelValue(DataArray[i]);
3                  }
4        Barrier();
5        for reduceLevel ← 1 to MaxReduceLevel {
6         for i ← 1 to n {
7                            if (NeedReduce(i, reduceLevel) ) {
8                                offset ← ComputeOffset(i, reduceLevel);
9                                LocalValue[i] ← Reduce(LocalValue[i], LocalValue[i+offset]);
10                               }
11                        }
12         Barrier();
13        }

In summary, the computation of the SVM classifier can be viewed as a composition of the pipe-and-filter, dense linear algebra, and MapReduce patterns. To parallelize the MapReduce computation, we used the data parallelism pattern. To implement the data parallelism Algorithmic Strategy, both the strict-data-parallel and loop-parallel patterns are applicable. We choose the strict-data-parallel pattern since it seemed a more natural choice given the fact we wanted to expose large amounts of concurrency for use on many-core chips with large numbers of cores. It is important to appreciate, however, that this is a matter of style and a quality design could have been produced using the loop- parallel pattern as well. To map the strict-data-parallel pattern onto a platform for execution, we chose SIMD pattern.  While we didn’t show the details of all the patterns used, along the way we used the shared-data pattern to define the synchronization protocols for the reduction and the collective synchronization pattern to describe the barrier construct. It is common that these functions (reduction and barrier) are provided as part of a parallel programming environment; hence, while a programmer needs to be aware of these constructs and what they provide, it is rare that they will need to explore their implementation in any detail.

Other Patterns

OPL is not complete. Currently OPL is restricted to those parts of the design process associated with architecting and implementing applications targeting parallel processors. There are countless additional patterns that software development teams utilize. Probably the best known example is the set of design patterns used in object-oriented design [Gamma94]. We made no attempt to include these in OPL. An interesting framework that supports common patterns in parallel object oriented design is TBB [Reinders07].

OPL focuses on patterns that are ultimately expressed in software. These patterns do not address, however, methodological patterns experienced parallel programmers use when designing or optimizing parallel software. The following are some examples of important classes of methodological patterns.

• Finding concurrency patterns [Mattson04]: These patterns capture the process that experienced parallel programmers use when exploiting the concurrency available in a problem. While these patterns were developed before our set of Computational Patterns was identified, they appear to be useful in moving from the Computational Patterns category of our hierarchy to the Parallel Algorithmic Strategy category. For example applying these patterns would help to indicate when geometric decomposition is chosen over data parallelism as a dense linear algebra problem moves toward implementation.
• Parallel programming “best practices” patterns: This describes a broad range of patterns we are actively mining as we examine the detailed work in creating highly-efficient parallel implementations. Thus, these patterns appear to be useful when moving from the Implementation Strategy patterns to the Concurrent Execution patterns. For example, we are finding common patterns associated with optimizing software to maximize data locality.

Summary, Conclusions and Future Work

We believe that the key to addressing the challenge of writing software is to architect the software. In particular, we believe that the key to addressing the new challenge of programming multicore and manycore processors is to carefully architect the parallel software. We can define a systematic methodology for software architecture in terms of design patterns and a pattern language. Toward this end we have taken on the ambitious project of creating a comprehensive pattern language that spans all the way from the initial software architecture of an application down to the lowest level details of software implementation.

OPL is a “work in progress”. We have defined the layers in OPL, listed the patterns at each layer, and written text for many of the patterns. Details are available online [OPL]. On the one hand, much work remains to be done. On the other hand, we do feel confident that our structural patterns capture the critical ways of composing software and our computational patterns capture the key underlying computations. Similarly, as we move down through the pattern language we feel that the patterns at each layer do a good job of addressing most of the key problems for which they are intended. The current state of the textual descriptions of the patterns in OPL is somewhat nascent. We need to finish  writing the text for some of the patterns and have them carefully reviewed by experts in parallel applications programming. We also need to continue mining patterns from existing parallel software to identify patterns that may be missing from our language. Nevertheless, last year’s effort spent in mining five applications netted (only) three new patterns for OPL. This shows that while OPL is not fully complete, it is not, with the caveats described in Section 5, dramatically deficient.

Complementing the efforts to mine existing parallel applications for patterns is the process of architecting new applications using OPL. We are currently using OPL to architect and implement a number of applications in areas such as machine learning, computer vision, computational finance, health, physical modeling, and games. During this process we are watching carefully to identify where OPL helps us and where OPL does not offer patterns to guide the kind of design decisions we must make. For example, mapping a number of computer-vision applications to new generations of manycore architectures helped identify the importance of a family of data layout patterns.

OPL is an ambitious project. Its scope stretches across the full range of activities in architecting a complex application. It has been suggested that we have taken on too large of a task; that it is not possible to define the complete software design process in terms of a single design pattern language. However, after many years of hard work nobody has been able to solve the parallel programming problem with specialized parallel programming languages or tools that automate the parallel programming process. We believe a different approach is required; one that emphasizes how people think about algorithms and design software. This is precisely the approach supported by design patterns, and based on our results so far we believe that patterns and a pattern language may indeed be the key to finally resolving the parallel programming problem.

While this claim may seem grandiose, we have an even greater aim for our work. We believe that our efforts to identify the core computational and structural patterns for parallel programming has led us to begin to identify the core computational elements (computational patterns, analogous to atoms) and means of assembling them (structural patterns, analogous to molecular bonding) of all electronic system. If this is true then these patterns not only serve as a means to assist software design but can be used to architect a curriculum for a true discipline of computer science.

References

[Alexander77] C. Alexander, S. Ishikawa, M. Silverstein, A Pattern Language: Towns, Buildings, Construction, Oxford University Press, 1977.

[Asanovic06] K. Asanovic, et al, “The landscape of parallel computing research: A view from Berkeley,” EECS Department, University of California, Berkeley, Tech. Rep. UCB/EECS-2006-183, 2006.

[Asanovic09] K. Asanovic, R. Bodik, J. Demmel, T. Keaveny, K. Keutzer, J. Kubiatowicz, N. Morgan, D. Patterson, K. Sen, J. Wawrzynek, D. Wessel, and K. Yelick, “A View of the Parallel Computing Landscape”, Submitted to Communications of the ACM, May 2008, to appear in 2009.

[Buschmann96] F. Buschmann, R. Meunier, H. Rohnert, P. Sommerlad, and M. Stal, Pattern-Oriented Software Architecture – A System of Patterns. Wiley 1996.

[Dean04] J. Dean and S. Ghemawat, “MapReduce: Simplified Data Processing on Large Clusters,” in Proceedings of OSDI ’04: 6th Symposium on Operating System Design and Implemention, San Francisco, CA, Dec. 2004.

[Gamma94] E. Gamma, R. Helm, R. Johnson, and J. Vlissides, “Design Patterns: Elements of reusable Object Oriented Software, Addison-Wesley, 1994.

[Garlan94] D. Garlan and M. Shaw. An introduction to software architecture. Technical report, Pittsburgh, PA, USA, 1994.

[Hwu08] W-M. Hwu, K. Keutzer, T. Mattson, “The Concurrency Challenge,” IEEE Design and Test, 25, 4, 2008. pp. 312 – 320.

[Mattson04] T. G. Mattson, B. A. Sanders, B. L. Massingill, Patterns for Parallel Programming, Addison Wesley, 2004.

[OPL09]     http://parlab.eecs.berkeley.edu/wiki/patterns/patterns

[Reinders07] J. Reinders, Intel Threaded Building Blocks, O’Reilly Press, 2007. [Shaw95] Mary Shaw and David Garlan. Software Architecture: Perspectives on an Emerging Discipline. Prentice Hall, 1995.

[Valiant90] L. G. Valiant, “A Bridging Model for parallel Computation”, Communication of the ACM, vol, 33, pp. 103-111, 1990.

Appendix: Design pattern Descriptions

In this appendix, we will describe the contents of each category of patterns within OPL. For each category of patterns, we will define the goal of the patterns within that category, the artifacts from the design process produced with this category of patterns, the activities associated with these patterns, and finally the patterns themselves.

Structural patterns

Goal: These patterns define the overall structure for a program.

Output: The overall organization of a program; often represented as an informal picture of a program’s high level design. These are the “boxes and arcs” a software architect would write on a whiteboard in describing their design of an application.

Activities: The basic program structure is identified from among the structural patterns. Then the architect examines the “boxes” of the program structure to identify computational kernels.

• Pipe-and-filter: These problems are characterized by data flowing through modular phases of computation. The solution constructs the program as filters (computational elements) connected by pipes (data communication channels). Alternatively, they can be viewed as a graph with computations as vertices and communication along edges.  Data flows through the succession of stateless filters, taking input only from its input pipe(s), transforming that data, and passing the output to the next filter via its output pipe
• Agent and Repository: These problems are naturally organized as a collection of data elements that are modified at irregular times by a flexible set of distinct operations. The solution is to structure the computation in terms of a single centrally-managed data repository, a collection of autonomous agents that operate upon the data, and a manager that schedules the agents’ access to the repository and enforces consistency.
• Process control: Many problems are naturally modeled as a process that either must be continuously controlled; or must be monitored until completion. The solution is to define the program analogously to a physical process control pipeline: sensors sense the current state of the process to be controlled; controllers determine which actuators are to be affected; actuators actuate the process. This process control may be continuous and unending (e.g. heater and thermostat), or it may have some specific termination point (e.g. production on assembly line).
• Event-based implicit invocation: Some problems are modeled as a series of processes or tasks which respond to events in a medium by issuing their own events into that medium. The structure of these processes is highly flexible and dynamic as processes may know nothing about the origin of the events, their orientation in the medium, or the identity of processes that receive events they issue. The solution is to represent the program as a collection of agents that execute asynchronously: listening for events in the medium, responding to events, and issuing events for other agents into the same medium. The architecture enforces a high level abstraction so invocation of an event for an agent is implicit; i.e. not hardwired to a specific controlling agent.

• Model-view-controller: Some problems are naturally described in terms of an internal data model, a variety of ways of viewing the data in the model, and a series of user controls that either change the state of the data in the model or select different views of the model. While conceptually simple, such systems become complicated if users can directly change the formatting of the data in the model or view-renderers come to rely on particular formatting of data in the model. The solution is to segregate the software into three modular components: a central data model which contains the persistent state of the program; a controller that  manages updates of the state; and one or more agents that export views of the model. In this solution the user cannot modify either the data model or the view except through public interfaces of the model and view respectively. Similarly the view renderer can only access data through a public interface and cannot rely on internals of the data model.
• Iterative refinement: Some problems may be viewed as the application of a set of operations over and over to a system until a predefined goal is realized or constraint is met. The number of applications of the operation in question may  not be predefined, and the number of iterations through the loop may not be able to be statically determined.  The solution to these problems is to wrap a flexible iterative framework around the operation that operates as follows: the iterative computation is performed; the results are checked against a termination condition; depending on the results of the check, the computation completes or proceeds to the next iteration.
  • Map reduce: For an important class of problems the same function may be applied to many independent data sets and the final result is some sort of summary or aggregation of the results of that application. While there are a variety of ways to structure such computations, the problem is to find the one that best exploits the computational efficiency latent in this structure. The solution is to define a program structured as two distinct phases. In phase one a single function is mapped onto independent sets of data. In phase two the results of mapping that function on the sets of data are reduced. The reduction may be a summary computation, or merely a data reduction.
  • Layered systems: Sophisticated software systems naturally evolve over time by building more complex operations on top of simple ones. The problem is that if each successive layer comes to rely on the implementation details of each lower layer then such systems soon become ossified as they are unable to easily evolve. The solution is to structure the program as multiple layers in such a way that enforces a separation of concerns. This separation should ensure that: (1) only adjacent layers interact and (2) interacting layers are only concerned with the interfaces presented by other layers. Such a system is able to evolve much more freely.
  • Puppeteer: Some problems require a collection of agents to interact in potentially complex and dynamic ways. While the agents are likely to exchange some data and some reformatting is required, the interactions primarily involve the coordination of the agents and not the creation of persistent shared data. The solution is to introduce a manager to coordinate the interaction of the agents, i.e. a puppeteer, to centralize the control over a set of agents and to manage the interfaces between the agents.
  • Arbitrary static task graph: Sometimes it’s simply not clear how to use any of the other structural patterns in OPL, but still the software system must be architected. In this case, the last resort is to decompose the system into independent tasks whose pattern of interaction is an arbitrary graph. Since this must be expressed as a fixed software structure, the structure of the graph is static and does not change once the computation is established.

Computational patterns

Goal: These patterns define the computations carried out by the components that make up a program.

Output: Definitions of the types of computations that will be carried out. In some cases, specific library routines will be defined.

Activities: The key computational kernels are matched with computational patterns. Then the architect examines how the identified computational patterns should be implemented. This may lead to another iteration through structural patterns, or a move downward in the hierarchy to algorithmic strategy patterns.

• Backtrack, branch and bound: Many problems are naturally expressed as either the search over a space of variables to find an assignment of values to the  variables that resolves a Yes/No question (a decision procedure) or assigns values to the variables that gives a maximal or minimal value to a cost function over the variables, respecting some set of constraints. The challenge is to organize the search such that solutions to the problem, if they exist, are found, and the search is performed as computationally efficiently as possible. The solution strategy for these problems is to impose an organization on the space to be searched that allows for sub-spaces that do not contain solutions to be pruned as early as possible.

• Circuits: Some problems are best described as Boolean operations on individual Boolean values or vectors (bit-vectors) of Boolean values. The most direct solution is to represent the computation as a combinational circuit and, if persistent state is required in the computation, to describe the computation as a sequential circuit: that is, a mixture of combinational circuits and memory elements (such as flip-flops).
• Dynamic programming: Some search problems have the additional characteristic that the solution to a problem of size N can always be assembled out of solutions to problems of size ≤ N-1. The solution in this case is to exploit this property to efficiently explore the search space by finding solutions incrementally and not looking for solutions to larger problems until the solutions to relevant sub- problems are found.
• Dense linear algebra: A large class of problems expressed as linear operations applied to matrices and vectors for which most elements are non-zero.  a computation is organized as a sequence of arithmetic expressions acting on dense arrays of data. The operations and data access patterns are well defined mathematically so data can be pre-fetched and CPUs execute close to their theoretically allowed peak performance. Applications of this pattern typically use standard building defined in terms of the dimensions of the dense arrays with vectors (BLAS level 1), matrix-vector
• Sparse Linear Algebra: This includes a large class of problems expressed in terms of linear operations over sparse matrices (i.e. matrices for which it is advantages to explicitly take into account the fact that many elements are zero).  Solutions are diverse and include a wide range of direct and iterative methods.
• Finite state machine: Some problems have the character that a machine needs to be constructed to control or arbitrate a piece of real or virtual machinery. Other problems have the character that an input string needs to be scanned for syntactic correctness. Both problems can be solved by creating a finite-state machine that monitors the sequence of input for correctness and may, optionally, produce intermediate output.
• Graph algorithms: A broad range of problems are naturally represented as actions on graphs of vertices and edges. Solutions to this class of problems involve building the representation of the problem as a graph, and applying the  appropriate graph traversal or partitioning algorithm that results in the desired computation.
• Graphical models: Many problems are naturally represented as graphs of random variables, where the edges represent correlations between variables. Typical problems include inferring probability distributions over a set of hidden states, given observations on a set of observed states observed states, or estimating the most likely state of a set of hidden states, given observations. To address this broad class of problems is an equally broad set of solutions known as graphical models.

• Monte Carlo: Monte Carlo approaches use random sampling to understand properties of large sets of points. Sampling the set of points produces a useful approximation to the correct result.
• N-body: Problems in which the properties of each member of a system depends on the state of every other member of the system. For modest sized systems, computing each interaction explicitly for every point is feasible (a naïve O(N2) solution). In most cases, however, the arrangement of the members of the system in space is used to define an approximation scheme that produces an approximate

solution for a complexity less than the naïve solution.

• Spectral methods: These problems involve systems that are defined in terms of more than one representation. For example, a periodic sequence in time can be represented as a set of discrete points in time or as a linear combination of frequency components. This pattern addresses problems where changing the representation of a system can convert a difficult problem into a straightforward algebraic problem.  The solutions depend on an efficient mechanism to carry out the transformation such as a fast Fourier transform.
• Structured mesh: These problems represent a system in terms of a discrete sampling of points in a system that is naturally defined by a mesh. For a structured mesh, the points are tied to the geometry of the domain by a regular process. Solutions to these problems are computed for each point based on computations over neighborhoods of points (explicit methods) or as solutions to linear systems of equations (implicit methods)
• Unstructured mesh: Some problems that are based on meshes utilize meshes that are not tightly coupled to the geometry of the underlying problems.  In other words, these meshes are irregular relative to the problem geometry. The solutions are similar to those for the structured mesh (i.e. explicit or implicit) but in the sparse case, the computations require gather and scatter operations over sparse data.

Algorithm Strategy patterns

Goal: These patterns describe the high level strategies used when creating the parallel algorithms used to implement the computational patterns.

Output: Definition of the algorithms and choice of concurrency to be exploited. Activities: Once the pattern for a key computation is identified, there may be a variety of different ways to perform that computation. At this step the architect chooses which particular algorithm, or family of algorithms, will be used to implement this computation. Also, this is the stage where the opportunities for concurrency, which are latent in the computation, are identified. Trade-offs among different algorithms and strategies will be examined in attempt to identify the best match to the computation at hand.

• Task parallelism: These problems are characterized in terms of a collection of activities or tasks. The solution is to schedule the tasks for execution in a way that

keeps the work balanced between the processing elements of the parallel computer and manages any dependencies between tasks so the correct answer is produced regardless of the details of how the tasks execute. This pattern includes the well known embarrassingly parallel pattern (no dependencies).

• Pipeline: For these problems consist of a stream of data elements and a serial sequence of transformations to apply to these elements. On initial inspection, there appears to be little opportunity for concurrency. If the processing for each data element, however, can be carried out concurrently with that for the other data elements, the problem can be solved in parallel by setting up a series of fixed coarse-grained tasks (stages) with data flowing between them in an assembly-line like manner. The solution starts out serial as the first data element is handled, but with additional elements moving into the pipeline, concurrency grows up to the number of stages in the pipeline (the so-called depth of the pipeline)
• Discrete event: Some problems are defined in terms of a loosely connected sequence of tasks that interact at unpredictable moments.  The solution is to setup an event handler infrastructure of some type and then launch a collection of tasks whose interaction is handled through the event handler.  The handler is an intermediary between tasks, and in many cases the tasks do not need to know the source or destination for the events.  This pattern is often used for GUI design  and discrete event simulations.
• Speculation: The problem contains a potentially large number of tasks that can usually run concurrently; however, for a subset of the tasks unpredictable dependencies emerge and these make it impossible to safely let the full set of tasks run concurrently. An effective solution may be to just run the tasks independently, that is speculate that concurrent execution will be committed, and then clean up after the fact any cases where concurrent execution was incorrect. Two essential element of this solution are: 1) to have an easily identifiable safety check to determine whether a computation can be committed and 2) the ability to rollback and re-compute the cases where the speculation was not correct.
• Data parallelism: Some problems are best understood as parallel operations on the elements of a data structure. When the operations are for the most part uniformly applied to these elements, an effective solution is to treat the problem as a single stream of instructions applied to each element. This pattern can be extended to a wider range of problems by defining an index space and then aligning both the parallel operations and the data structures around each point in the index space.
• Recursive splitting: Sometimes, an algorithm can be expressed as the composition of a series of tasks that are generated recursively or generated during the traversal of a recursive data structure. The problem is how to efficiently execute such algorithms that might exhibit data dependent and dynamic task creation behavior with limited knowledge of the available hardware resources. The solution is to (1) Express problem recursively with more than one task generated per call (2) Use a balanced data structure, if possible (3) Use a fork-join or task-queue implementation (4) Use optimizations to improve locality.

• Geometric decomposition: An algorithm is organized by: (1) dividing the key data structures within a problem into regular chunks, and (2) updating each chunk in parallel. Typically, communication occurs at chunk boundaries so an algorithm breaks down into three components: (1) exchange boundary data, (2) update the interiors or each chunk, and (3) update boundary regions. The size of the chunks  is dictated by the properties of the memory hierarchy to maximize reuse of data from local memory/cache..

Implementation strategy patterns

Goal: These patterns focus on how a software architecture is implemented in software. They describe how threads or processes execute code within a program; i.e. they are intimately connected with how an algorithm design is implemented in source code. These patterns fall into two sets: program structure patterns and data structure patterns. Output: pseudo-code defining how a parallel algorithm will be realized in software. Activities: This is the stage where the broad opportunities for concurrency identified by the parallel algorithmic strategy patterns are mapped onto particular software constructs for implementing that concurrency. Advantages and disadvantages of different software constructs will be weighed.

• Program structure
  • Single-Program Multiple Data (SPMD): Keeping track of multiple streams of instructions can be very difficult for a programmer. If each instruction stream comes from independent source code, the software can quickly become unmanageable. There are a number of solutions to this problem. One is to have a single program (SP) that is used for all of the streams of instructions. An process/thread ID (or rank) is defined for each instance of the program and this can be used to index into multiple data sets (MD) or branch into different sub-sets of instructions.
  • Strict data parallel: Data parallel algorithms constitute a large class of algorithms depending on the details of how data is shared as operations are applied concurrently to the data. If the sharing is minimal or if it can be handled by well-defined collective operations (e.g. parallel pre-fix or shift and mask operations) it may be possible to solve the problem with a single stream of instructions applied to data elements concurrently. In other words, the concurrency is strictly represented as a single stream of instructions applied to parallel data structures.
  • Fork/join: The problem is defined in terms of a set of functions or tasks that execute within a shared address space.  The solution is to logically create threads (fork), carry out concurrent computations, and then terminate them after possibly combining results from the computations (join).
  • Actors: An important class of object oriented programs represents the state of the computation in terms of a set of persistent objects.  These objects encapsulate the state of the computation and include the fundamental operations to solve the problem as methods for the objects.  In these cases, an effective solution to the concurrency problem is to make these persistent objects distinct software agents (the actors) that interact over distinct channels (message passing).

• Master-worker: A common problem in parallel programming is how to balance the computational load among a set of processing elements within a parallel computer. For task parallel programs with no communication  between tasks (or infrequence but well-structured, anonymous  communication) and effective solution with “automatic dynamic load balancing” is to define a single master to mange the collection of tasks and collect results. Then a set of workers grab a task, do the work, send the results back to the master, and then grab the next task. This continues until all the tasks have been computed.
• Task queue: For task parallel problems with independent tasks, the challenge is how to schedule the execution of tasks to balance the computational load among the processing elements of a parallel computer. One solution is to place the tasks into a task queue. The runtime system then pulls tasks out of the queue, carries out the computations, then goes back to the queue for the next task. Notice that this is closely related too the master/worker pattern but in this case, there is no need for extra processing by a master to either manage the tasks or to deal with the results of the tasks. Also, unlike master-worker, task generation is not restricted to the master thread alone.
• Graph Partitioning: A graph is typically a single monolithic structure with edges indicating relations among vertices. The problem is how to organize concurrent computation on this single structure in such a way that computations on many parts of the graph can be done concurrently. The solution is to find a strategy for partitioning the graph such that synchronization is minimized and the workload is balanced.
• Loop-level parallelism: The problem is expressed in terms of a modest number of compute intensive loops. The loop iterations can be transformed so they can safely execute independently. The solution is to transform the loops as needed to support safe concurrent execution, and then replace the serial compute intensive loops with parallel loop constructs (such as the “for worksharing construct” in OpenMP). A common goal of these solutions is to create a single program that executes in serial using serial compilers or in parallel using compilers that understand the parallel loop construct.
• BSP: Managing computations and communications plus overlapping them to optimize performance can be very difficult. When the computations break down into a regular sequence of stages with well defined communication protocols between phases, a simplified computational structure can be used. One such structure is the BSP model of computation described in [Valiant90]. In this solutions, a computation is organized as a sequence of super-steps. Within a super-step, computation occurs on a local view of the data. Communication events are posted within a super-step but the results are not available until the subsequent super-step. Communication events from a super-step are guaranteed to complete before the subsequent super-step starts. This structure lets the supporting runtime system overlap communication and computation while making the overall program structure easier to understand.
• Data Structure Patterns
  • Shared queue: Some problems generate streams of results that must be handled in some predefined order. It can be very difficult to safely put items into the stream or pull them off the stream when concurrently executing tasks are involved. The solution is to define a shared queue where the safe management of the queue is built into the operations upon the queue.
  • Distributed array: The array is a critical data structure in many problems.

Operating on components of the array concurrently (for example, using the geometric decomposition pattern) is an effective way to solve these problems in parallel. Concurrent computations may be straightforward to define, but defining how the array is decomposed among a collection of processes or threads can be very difficult. In particular, solutions can require complex book-keeping to map indices between global indices in the original problem domain and local indices visible to a particular thread or process. The solution is to define a distributed array and fold the complicated index algebra into access methods on the distributed array data type. The programmer still needs to handle potentially complex index algebra, but it’s localized to one place and can possibly be reused across programs that use similar array data types.

• Shared hash table: A hash table is one an important data structure in a wide range of problems. It is particularly important in parallel algorithms as a wide range of distributed data structures can be mapped onto a hash table. As with the distributed array pattern, the problem is the indexing required to transform a global hash key into a local hash key for a particular member of the set of processes or threads involved with a parallel computation. The solution is to place the indexing operations inside a method associated with a hash table data type to insulate this complexity for the larger source code and support reuse between related program.
• Shared data: Programmers should always try to represent data shared between threads or processes as shared data types with a well defined API to hide the complexity of safe concurrent access to the data. In some cases, however, this just is not practical. The solution is to put data into a shared address space   and then define synchronization protocols to protect that data.

Parallel Execution Patterns

Goal: These patterns describe how a parallel algorithm is organized into software elements that execute on real hardware and interact tightly with a specific programming model. We organize these into two sets: (1) process/thread control patterns and (2) coordination patterns.

Output: Should produce particular approaches to exploit the hardware capabilities for parallelism so that we can execute programs efficiently.

Activities: This is the stage where the previously identified software constructs ware matched up with the actual execution capability of the underlying hardware. At this point the performance of the underlying hardware mechanisms may be known and the advantages and disadvantages of different mappings to hardware can be precisely measured.

• Patterns that “advance a program counter”
  • MIMD: The problem is expressed in terms of a set of tasks operating concurrently on their own streams of data. The solution is to construct the parallel program as sequential processes that execute independently and coordinate their execution through discrete communication events.
  • Data flow: When a problem is defined as a sequence of transformations applied to a stream of data elements, an effective parallel execution strategy is to organize the computation around the flow of data. The tasks become the nodes in a fixed network of sequential processes and the data flows through the network from one node to the other. Task-graph: Higher order structure to a problem can be used to help make a concurrent program easier to understand. In some cases, however, no such structure is apparent. In these cases, the computation can be viewed as a directed acyclic graph of threads or processes which can be mapped onto the elements of a parallel computer.   This is a very general pattern that can be used at a low level to support the other execution patterns.
  • Single-Instruction Multiple Data (SIMD): Some problems map directly onto a sequence of operations applied uniformly to a collection of data structures. These problems can be solved by applying a single stream of instructions that are executed “in lockstep” by a set of processing elements but on their own streams of data. Common examples are the vector instructions built into  many modern microprocessors.
  • Thread pool: Fork/Join and other patterns based on dynamic sets of threads may include frequent operations to create or destroy threads. This is a very expensive operation on most systems. The solution is to maintain a pool of threads. Instead of creating a new thread, a thread is used from the pool. Instead of destroying a thread (e.g. when a fork operations is encountered) the thread is returned to the pool. This approach is commonly used with task- queue programs with work stealing to enforce a more balanced load.
  • Speculative execution: Compilers and parallel runtime systems must make conservative assumptions about the data shared between tasks to assure that correct results are produced. This approach can overly constrain the concurrency available to a problem. The solution is to have a compiler or runtime system that is enabled for speculative execution. This means that additional concurrent tasks are exposed together with a way to test after the fact that speculation was safe and a way to rollback and re-compute unsafe results when speculation was not warranted.
  • Digital circuits: The implementation of system functionality is often so highly constrained that it cannot be entirely implemented in software and still meet speed or power constraints. One solution strategy for highly concurrent implementation is to implement functionality in digital circuits. These circuits may operate asynchronously as special-purpose execution units or they may be implemented as instruction extensions of a instruction-set processor.
  • Patterns that Coordinate the execution of threads or processes
    • Message passing: The problem is to coordinate the execution of a collection of processes or threads, but with no support from the hardware for data structures in a shared memory. The solution is to organize coordination operations (synchronization and communication) in terms of distinct messages passed over some sort of interconnection network.
    • Collective communication: Working directly with messages passed between pairs of processes/threads is error prone and can be difficult to understand. In some cases, you can avoid low level pair-wise communication by casting the problem in terms of communications operations over collections of processes/threads. Common examples include reductions, broadcasts, prefix sums, and scatter/gather.
    • Mutual exclusion: When executing on a shared address space machine, undisciplined mixtures of reads and writes can lead to race conditions (programs that yield different results as an OS makes different choices about how to schedule threads). In this case, the solution is to define blocks of code or updates of memory that can only be executed by one process or thread at a time.
    • Point to point synchronization: In some problems, pairs of threads have ordering constraints that must be satisfied to support race-free and correct results. In this case, a range of synchronization events such as a mutex are needed that operate just between pairs of threads.
    • Collective synchronization: Using synchronization to impose a partial order over a collection of threads is error prone and can result in programs riddled with race conditions. The solution is to wherever possible, to use higher level synchronization operations (such as barrier synchronization) to apply across collections of threads or processes.
    • Transactional memory: Writing race free programs can be a difficult problem on shared address space computers. This is particularly the case with relaxed memory models. The solution is to use either the point-to-point or collective synchronization patterns to protect blocks of code at a course level of granularity. This greatly restricts opportunities to exploit concurrency. Low level synchronization operations at a fine level of granularity can be used (using, for example, the shared data pattern) but these fine grained synchronization protocols are difficult to implement correctly. The solution is to use the high level concept of transactions and a transactional memory. The idea is to fold into the memory system the operations required to detect access conflicts and to rollback and reissue transactions when a conflict occurs.  The transactional memory lets a programmer avoid the complexity of fine grained locking, but, it is a speculative parallelism approach and is only effective  when data access conflicts are rare and the need to roll-back and reissue transactions is infrequent.